第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
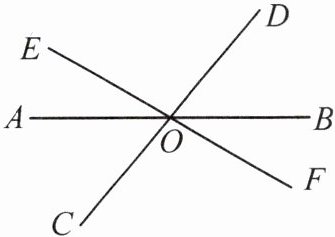
10. (清华附中校本经典题) 如图,直线 $ AB $,$ CD $,$ EF $ 相交于点 $ O $.
(1) 写出 $ \angle DOA $,$ \angle EOC $ 的对顶角;
(2) 如果 $ \angle AOC = 50^{\circ} $,求 $ \angle BOD $,$ \angle COB $ 的度数.
(1) 写出 $ \angle DOA $,$ \angle EOC $ 的对顶角;
(2) 如果 $ \angle AOC = 50^{\circ} $,求 $ \angle BOD $,$ \angle COB $ 的度数.

答案:
解:
(1)∠DOA的对顶角是∠COB,∠EOC的对顶角是∠DOF.
(2)
∵∠AOC=50°,
∴∠BOD=50°,∠COB=180°−50°=130°.
(1)∠DOA的对顶角是∠COB,∠EOC的对顶角是∠DOF.
(2)
∵∠AOC=50°,
∴∠BOD=50°,∠COB=180°−50°=130°.
11. 如图,取两根木条 $ a $,$ b $,将它们钉在一起,固定木条 $ a $,转动木条 $ b $,当 $ \angle 1 $ 增大 $ 4^{\circ} $ 时,下列说法正确的是(
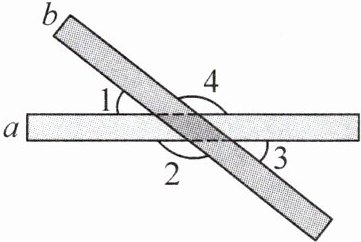
A.$ \angle 2 $ 增大 $ 4^{\circ} $
B.$ \angle 3 $ 增大 $ 4^{\circ} $
C.$ \angle 4 $ 增大 $ 4^{\circ} $
D.$ \angle 4 $ 减小 $ 2^{\circ} $
B
)
A.$ \angle 2 $ 增大 $ 4^{\circ} $
B.$ \angle 3 $ 增大 $ 4^{\circ} $
C.$ \angle 4 $ 增大 $ 4^{\circ} $
D.$ \angle 4 $ 减小 $ 2^{\circ} $
答案:
B
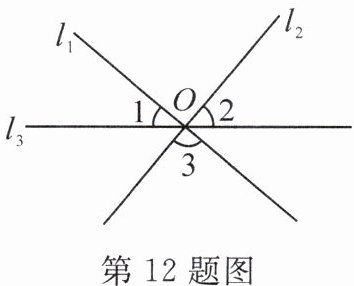
12. (兰生复旦校本经典题) 如图,直线 $ l_1 $,$ l_2 $,$ l_3 $ 相交于点 $ O $,$ \angle 1 = 40^{\circ} $,$ \angle 2 = 50^{\circ} $,则 $ \angle 3 $ 的度数为
90°
.
答案:
90°
13. 如图所示,直线 $ a $,$ b $,$ c $ 两两相交,$ \angle 1 = 60^{\circ} $,$ \angle 2 = \frac{2}{3} \angle 4 $,则 $ \angle 3 = $
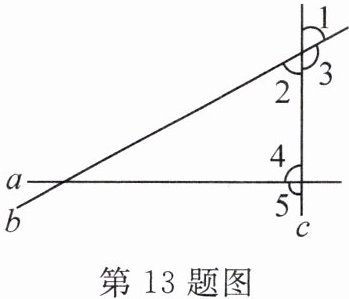
120°
,$ \angle 5 = $90°
.
答案:
120° 90°
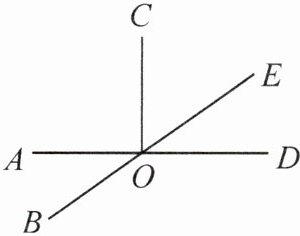
14. 如图,已知直线 $ AD $,$ BE $ 相交于点 $ O $,$ \angle DOE $ 与 $ \angle COE $ 互余,$ \angle COE = 55^{\circ} $,求 $ \angle AOB $ 的度数.

答案:
解:
∵∠DOE与∠COE互余,
∴∠COE+∠EOD=90°.
∵∠COE =55°,
∴∠DOE=90°−∠COE=35°.
∴∠AOB=∠DOE=35°.
∵∠DOE与∠COE互余,
∴∠COE+∠EOD=90°.
∵∠COE =55°,
∴∠DOE=90°−∠COE=35°.
∴∠AOB=∠DOE=35°.
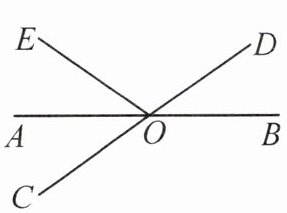
15. (人大附中校本经典题) 如图,直线 $ AB $,$ CD $ 相交于点 $ O $,$ OA $ 平分 $ \angle EOC $.
(1) 若 $ \angle EOC = 70^{\circ} $,求 $ \angle BOD $ 的度数;
(2) 若 $ \angle EOC : \angle EOD = 2 : 3 $,求 $ \angle BOD $ 的度数.
(1) 若 $ \angle EOC = 70^{\circ} $,求 $ \angle BOD $ 的度数;
(2) 若 $ \angle EOC : \angle EOD = 2 : 3 $,求 $ \angle BOD $ 的度数.

答案:
解:
(1)
∵OA平分∠EOC,∠EOC=70°,
∴∠AOE=∠AOC=$\frac{1}{2}$∠EOC=35°.
∵∠AOC=∠BOD,
∴∠BOD=35°.
(2)
∵∠EOC :∠EOD=2:3,∠EOC+∠EOD=180°,
∴∠EOC=180°×$\frac{2}{5}$=72°,∠EOD=180°×$\frac{3}{5}$=108°.
∵OA平分∠EOC,
∴∠AOE=∠AOC=$\frac{1}{2}$∠EOC=36°.
∵∠AOC=∠BOD,
∴∠BOD=36°.
(1)
∵OA平分∠EOC,∠EOC=70°,
∴∠AOE=∠AOC=$\frac{1}{2}$∠EOC=35°.
∵∠AOC=∠BOD,
∴∠BOD=35°.
(2)
∵∠EOC :∠EOD=2:3,∠EOC+∠EOD=180°,
∴∠EOC=180°×$\frac{2}{5}$=72°,∠EOD=180°×$\frac{3}{5}$=108°.
∵OA平分∠EOC,
∴∠AOE=∠AOC=$\frac{1}{2}$∠EOC=36°.
∵∠AOC=∠BOD,
∴∠BOD=36°.
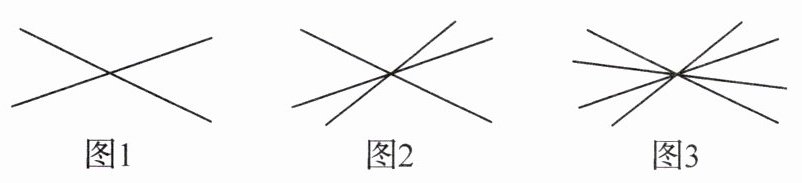
16. (新考向 推理能力) 观察下列图形,寻找对顶角(不含平角).
【特例分析】
(1) 如图 1,两条直线相交于一点,共有
【规律总结】
(2) 根据填空结果探究:当 $ n $ 条直线相交于一点时,共有
【规律应用】
(3) 根据探究结果,求 1 000 条直线相交于一点时,所构成的对顶角的对数.
【特例分析】
(1) 如图 1,两条直线相交于一点,共有
2
对对顶角;如图 2,三条直线相交于一点,共有6
对对顶角;如图 3,四条直线相交于一点,共有12
对对顶角;【规律总结】
(2) 根据填空结果探究:当 $ n $ 条直线相交于一点时,共有
n(n−1)
对对顶角;【规律应用】
(3) 根据探究结果,求 1 000 条直线相交于一点时,所构成的对顶角的对数.

答案:
解:
(1)2 6 12
(2)n(n−1)
(3)1000条直线相交于一点时,所构成的对顶角的对数为1000×999=999000.
(1)2 6 12
(2)n(n−1)
(3)1000条直线相交于一点时,所构成的对顶角的对数为1000×999=999000.
查看更多完整答案,请扫码查看


