第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
11. 如图所示的图形是下列哪个几何体的俯视图(

C
)
答案:
C
12. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时,两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是(


D
)

答案:
D
13. 如图所示的是焦作市博物馆的四件特色藏品,其中主视图与左视图相同的是(

A
)
答案:
A
14. 新考向 数学文化 如图所示的图形出自《九章算术》“商功”卷,在互相垂直的墙体角落里,堆放着粟谷,将谷堆看作圆锥的一部分,则该谷堆的主视图为(
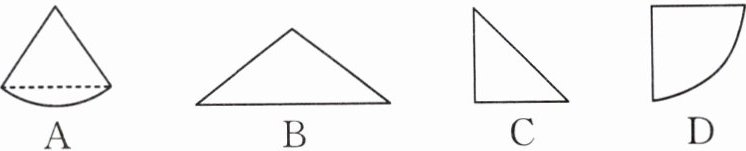

C
)

答案:
C
15. 如图所示的几何体是由相同大小的正方体积木堆叠而成,则拿走图中的哪一个积木后,此几何体主视图的形状会改变(
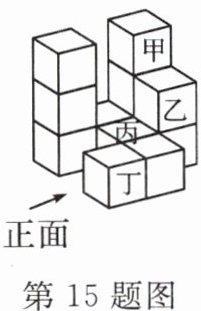
A.甲
B.乙
C.丙
D.丁
B
)
A.甲
B.乙
C.丙
D.丁
答案:
B
16. 如图,这是由十个小正方体组成的几何体.若每个小正方体的棱长都是2,则该几何体的主视图和左视图的面积之和是
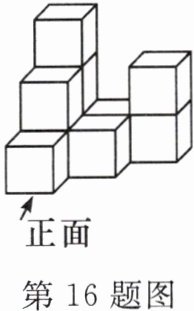
48
.
答案:
48
17. (2024·平顶山汝州市期中)用9个大小相同的小正方体搭成如图所示的几何体.
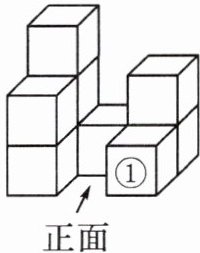
(1)请在方格中画出该几何体的三视图(不需要标序号①);
(2)将小正方体①移走后,得到一个新的几何体,则与原几何体相比,新几何体的三视图没有发生变化的是
A. 主视图和俯视图
B. 左视图和俯视图
C. 主视图和左视图
D. 主视图、左视图和俯视图
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,那么最多可以再添加


(1)请在方格中画出该几何体的三视图(不需要标序号①);
(2)将小正方体①移走后,得到一个新的几何体,则与原几何体相比,新几何体的三视图没有发生变化的是
C
;A. 主视图和俯视图
B. 左视图和俯视图
C. 主视图和左视图
D. 主视图、左视图和俯视图
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,那么最多可以再添加
2
个小正方体.
答案:
(1)
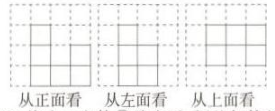
(2)C
(3)2
(1)

(2)C
(3)2
查看更多完整答案,请扫码查看


