《2025年名校课堂七年级数学上册华师大版河南专版》

【例】已知 $a,b,c$ 在数轴上的对应点的位置如图所示,且 $|a| = |c|$.
(1)填空: $a + b$ $0$ ; $c + a$ $0$ ; $c - b$ $0$ ;
(2)化简: $|a - b|+|b + c|-|c + a|-|a - c|$.

答案： [例]解:
(1)＜　=　＞　
(2)由题意,得a−b＞0,b+c＜0,c+α=0,α−c＞0,
∴原式=a−b+[−(b+c)]−0−(a−c)=a−b−b−c−0 −a+c=−2b.

1. 有理数 $a,b$ 在数轴上的对应点的位置如图所示,则化简 $|a+ b|+a$ 的结果是.

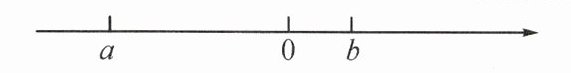
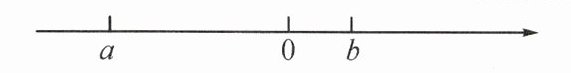
答案： 1. 由数轴知：$a ＜ 0$，$b ＞ 0$，且$|a| ＞ |b|$，则$a + b ＜ 0$，
$\therefore |a + b| = -(a + b)$，
$\therefore |a + b| + a = -(a + b) + a = -a - b + a = -b$。
结果：$-b$。

2. 已知数 $a,b,c$ 在数轴上的对应点的位置如图所示,则化简 $|a|+|a + b|-|c|$ 的结果是______.

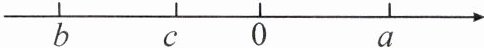
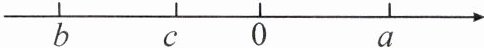
答案：

2. 由数轴知：$b ＜ c ＜ 0 ＜ a$，且$|b| ＞ a$，则$a + b ＜ 0$，

$\therefore |a| = a$，$|a + b| = -(a + b)$，$|c| = -c$，

$\therefore |a| + |a + b| - |c| = a + [-(a + b)] - (-c) = a - a - b + c = c - b$。

结果：$c - b$。

3. (2024·郑州四中期末)已知 $a,b,c$ 在数轴上的位置如图所示,则化简 $|a + c|-|a - 2b|-|c - 2b|$ 的结果是 ()

A.$0$
B.$4b$
C.$-2a - 2c$
D.$2a - 4b$

答案： B

【例】【教材呈现】“整体思想”是数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.下题是华师版七年级上册数学教材 P120 习题 T13.
代数式 $x^{2}+x + 3$ 的值为 $7$,则代数式 $2x^{2}+2x - 3$ 的值为.
【阅读理解】小明在做作业时采用的方法如下:由题意,得 $x^{2}+x + 3 = 7$,则 $x^{2}+x = 4$.所以 $2x^{2}+2x - 3 = 2(x^{2}+x)-3 = 2×4 - 3 = 5$.
【方法运用】
(1)若代数式 $x^{2}+x + 1$ 的值为 $15$,求代数式 $-2x^{2}-2x + 3$ 的值;
(2)当 $x = 2$ 时,代数式 $ax^{3}+bx + 4$ 的值为 $11$,求当 $x = -2$ 时,代数式 $ax^{3}+bx + 3$ 的值;
【拓展应用】
(3)若 $3m - 4n = -3,mn = -1$,求 $6(m - n)-2(n - mn)$ 的值.

答案：

[例]解:
(1)
∵x²+x+1=15,
∴x²+x=14.
∴−2x²−2x+3=−2(x²+x)+3=−2×14+3=−25.

(2)由题意,得8a+2b+4=11,
∴8a+2b=7.
∴当x=−2时,ax²+bx+3=−8a−2b+3=−(8a+2b)+3=−7+3=−4.

(3)
∵3m−4n=−3,mn=−1,

∴6(m−n)−2(n−mn)=6m−6n−2n+2mn=6m−8n+2mn=2(3m−4n)+2mn=2×(−3)+2×(−1)=−8.

1. (2024·南阳唐河县期中)已知 $a^{2}+3a - 4 = 0$,则代数式 $2a^{2}+6a - 11$ 的值为-3.

答案： -3

2. (2024·南阳内乡县期末)若整式 $xy - 2y^{3}+2$ 的值为 $5$,则整式 $-3xy + 6y^{3}-8$ 的值为-17.

答案： -17

3. 当 $x = 1$ 时,$ax^{3}-bx - 5$ 的值是 $2022$,则当 $x = -1$ 时,$ax^{3}-bx - 5$ 的值是-2032.

答案： -2032

4. (2023·沈阳)当 $a + b = 3$ 时,代数式 $2(a + 2b)-(3a + 5b)+5$ 的值为2.

答案： 2