《2025年名校课堂七年级数学上册华师大版河南专版》

11. (2023·郑州期末)如图，$\angle AOB = 68^{\circ}$，OC平分$\angle AOD$，$\angle COD = 15^{\circ}$，则$\angle BOD$的度数为(B)

A.$28^{\circ}$
B.$38^{\circ}$
C.$48^{\circ}$
D.$53^{\circ}$

答案： B

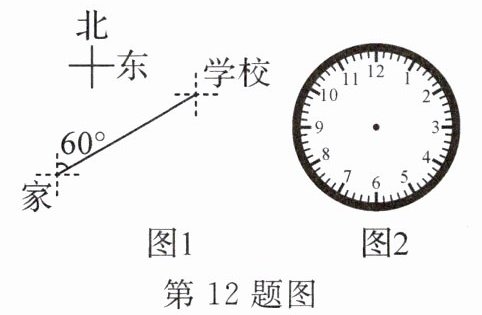
12. 如图1，小萍从地图上测得学校在她家的北偏东$60^{\circ}$方向，她看到家里的钟表表盘如图2所示.若把家的位置看成钟表表盘的中心，则她可以说学校在家的(B)

A.1点钟方向
B.2点钟方向
C.7点钟方向
D.8点钟方向

答案： B

13. (2024·开封杞县期末)如图，将一副三角板叠放在一起，使它们的直角顶点重合.
(1)若$\angle DCE = 35^{\circ}$，求$\angle ACB$的度数；
(2)若$\angle ACB = 140^{\circ}$，求$\angle DCE$的度数；
(3)猜想$\angle ACB$与$\angle DCE$之间的数量关系，并说明理由.

答案： 解:
(1)由题意可知,∠ACD=∠BCE=90°.
∵∠DCE=35°,
∴∠ACE=∠ACD-∠DCE=90°-35°=55°.
∴∠ACB=∠BCE+∠ACE=90°+55°=145°.
(2)
∵∠ACB=140°,∠ACD=90°,
∴∠BCD=∠ACB-∠ACD=140°-90°=50°.
∵∠BCE=90°,
∴∠DCE=∠BCE-∠BCD=90°-50°=40°.
(3)∠ACB+∠DCE=180°.理由如下:由题意,得∠ACD=∠ACE+∠DCE=90°,∠BCE=∠BCD+∠DCE=90°,
∴∠ACE+∠DCE+∠BCD+∠DCE=180°,即∠ACB+∠DCE=180°.

14. (2023·南阳桐柏县期末)若一个角的补角是$120^{\circ}$，则这个角的余角的度数是(A)

A.$30^{\circ}$
B.$60^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$

答案： A

15. (2024·南阳十九中月考)已知$\angle 1$是锐角，$\angle 1$与$\angle 2$互补，$\angle 1$与$\angle 3$互余，则$\angle 2 - \angle 3 =$(C)

A.$45^{\circ}$
B.$60^{\circ}$
C.$90^{\circ}$
D.$180^{\circ}$

答案： C

16. (2023·郑州管城区期末)如图，有公共端点P的两条线段MP，NP组成一条折线MPN.若该折线MPN上一点Q把这条折线分成相等的两部分，则把这个点Q叫做这条折线的“折中点”.已知D是折线ACB的“折中点”，E为线段AC的中点，$CD = 1$，$CE = 3$，则线段BC的长为8或4.

答案： 8或4

17. (2023·漯河临颍县期末)综合与实践
特例感知：
(1)如图1，已知线段$AB = 14cm$，C为线段AB上的一个动点，D，E分别是AC和BC的中点.
①若$AC = 4cm$，则线段$DE =$7cm；
②若$AC = a cm(a ＜ 14)$，则线段$DE =$7cm；
知识迁移：
(2)我们发现角的很多规律和线段一样，如图2，若$\angle AOB = 120^{\circ}$，OC是$\angle AOB$内部的一条射线，射线OM平分$\angle AOC$，射线ON平分$\angle BOC$，求$\angle MON$的度数；
拓展探究：
(3)已知$\angle COD$在$\angle AOB$内部的位置如图3所示，$\angle AOB = \alpha(\alpha ＜ 180^{\circ})$，$\angle COD = 30^{\circ}$，且$\angle DOM = 2\angle AOM$，$\angle CON = 2\angle BON$，则$\angle MON =$$(\frac{2}{3}\alpha+10)$°(用含$\alpha$的代数式表示).

答案： 解:
(1)①7 ②7
(2)
∵OC是∠AOB内部的一条射线,射线OM平分∠AOC,射线ON平分∠BOC,
∴∠CON=$\frac{1}{2}$∠BOC,∠COM=$\frac{1}{2}$∠AOC.
∵∠AOB=120°,
∴∠MON=∠CON+∠COM=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB=60°.
(3)$(\frac{2}{3}\alpha+10)$