《2025年名校课堂七年级数学上册华师大版河南专版》

10. (清华附中校本经典题) 如图，已知 $ ON \perp l $，$ OM \perp l $，所以 $ OM $ 与 $ ON $ 重合，其理由是(B)

A.两点确定一条直线
B.同一平面内，过一点有且只有一条直线与已知直线垂直
C.在同一平面内，过一点只能作一条垂线
D.两点之间线段最短

答案： B

11. (2024·郑州荥阳市期末) 如图，点 $ O $ 在直线 $ AB $ 上，$ OC \perp OD $ 于点 $ O $. 若 $ \angle BOD = 3 \angle BOC $，则 $ \angle AOD $ 的度数为(A)

A.$ 112.5^{\circ} $
B.$ 115^{\circ} $
C.$ 117.5^{\circ} $
D.$ 125^{\circ} $

答案： A

12. 如图，$ \angle BAC = 90^{\circ} $，$ AD \perp BC $，垂足为 $ D $，则下面的结论正确的有①④.(填序号)
① $ AB $ 与 $ AC $ 互相垂直；② $ AD $ 与 $ AC $ 互相垂直；③点 $ C $ 到 $ AB $ 的垂线段是线段 $ AB $；④线段 $ AB $ 的长度是点 $ B $ 到 $ AC $ 的距离；⑤线段 $ AB $ 是点 $ B $ 到 $ AC $ 的距离.

答案： ①④

13. (教材 P181 习题 T6 变式) 如图，按下述口令画出图形：将位于图中点 $ A $ 处的小海龟向上前进 3 格，然后向右转 $ 90^{\circ} $，前进 2 格；然后向右转 $ 90^{\circ} $，前进 3 格；然后向左转 $ 90^{\circ} $，前进 1 格；再向左转 $ 90^{\circ} $，前进 4 格，再向左转 $ 90^{\circ} $，前进 3 格；然后向右转 $ 90^{\circ} $，前进 3 格；然后向左转 $ 90^{\circ} $，前进 1 格；然后向左转 $ 90^{\circ} $，前进 7 格；再向左转 $ 90^{\circ} $，前进 1 格. 将小海龟经过的路线描出来，看一看是什么图形.

答案：

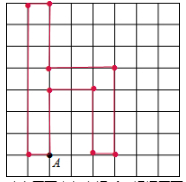
小海龟经过的路线是字母h.

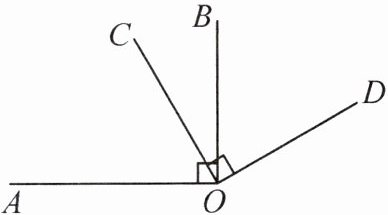
14. (湖南师大附中校本经典题) (1) 如图，$ \angle AOC = 60^{\circ} $，$ BO \perp OA $，$ CO \perp OD $，求 $ \angle AOD + \angle BOC $ 的度数；
(2) 如果将(1)中“$ \angle AOC = 60^{\circ} $”这个条件去掉，其他条件不变，还能求出 $ \angle AOD + \angle BOC $ 的度数吗？请说明理由.

答案： 解:
(1)
∵∠AOC=60°,BO⊥OA,
∴∠BOC=90°−60°=30°.
∵CO ⊥OD,
∴∠COD=90°.
∴∠AOD=∠COD+∠AOC=90°+60°=150°.
∴∠AOD+∠BOC=150°+30°=180°.
(2)能.理由如下:
∵BO⊥OA,CO⊥OD,
∴∠AOB=90°,∠COD=90°.
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=(∠AOC+∠BOC)+∠COD=∠AOB+∠COD=90°+90°=180°.

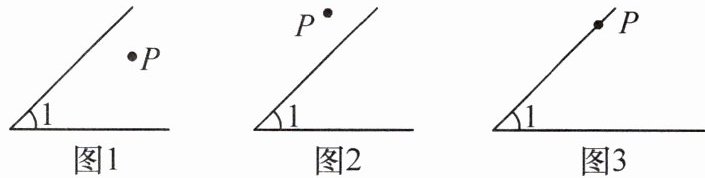
15. (新考向 推理能力) (1) 在图 1 中，过点 $ P $ 分别向 $ \angle 1 $ 的两边作垂线段，两条垂线段所形成的角为 $ \angle \alpha $；
(2) 量一量 $ \angle \alpha $ 与 $ \angle 1 $ 的度数，它们之间的数量关系是∠α+∠1=180°；
(3) 同样在图 2 和图 3 中过点 $ P $ 分别向 $ \angle 1 $ 的两边作垂线，两垂线的夹角为 $ \angle \alpha $，分别写出图 2 和图 3 中 $ \angle \alpha $ 和 $ \angle 1 $ 之间的数量关系；
(4) 由上述三种情形可以得到一个结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角相等或互补(不要求写出理由).

答案：
解:
(1)

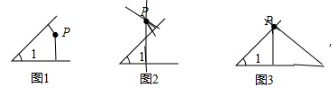
(2)∠α+∠1=180°　
(3)如图2,∠α=∠1或∠α+∠1=180°.如图3,∠α=∠1或∠α+∠1=180°.
(4)相等或互补