《2025年名校课堂七年级数学上册华师大版河南专版》

3. (2023·南阳方城县期末)已知$a^{2}+b^{2}=5$，$ab = -2$，求代数式$2(4a^{2}+2ab - b^{2})-3(5a^{2}-3ab + 2b^{2})+b^{2}$的值。

答案： 原式=8a² + 4ab - 2b² - 15a² + 9ab - 6b² + b² = -7a² - 7b² + 13ab = -7(a² + b²) + 13ab。当a² + b² = 5,ab = -2时，原式=-7×5 + 13×(-2)= -35 - 26 = -61。

4. 小丽放学回家后准备解决下面的题目：化简$(□ x^{2}-6x + 8)+(6x - 5x^{2}-2)$。她发现系数“$□$”印刷不清楚。
(1) 她把“$□$”猜成$3$，请化简：$(3x^{2}-6x + 8)+(6x - 5x^{2}-2)$；
(2) 她妈妈说：“你猜错了，我看到该题的标准答案是$6$。”请通过计算说明原题中“$□$”是几。

答案：
(1)原式=3x² - 6x + 8 + 6x - 5x² - 2 = -2x² + 6。
(2)设“□”是a。则原式=(ax² - 6x + 8) + (6x - 5x² - 2)=ax² - 6x + 8 + 6x - 5x² - 2=(a - 5)x² + 6。
∵标准答案是6，
∴a - 5 = 0，解得a = 5。
∴原题中“□”是5。

5. 如图，我们约定，上方相邻两代数式之和等于这两个代数式下方箭头共同指向的代数式。

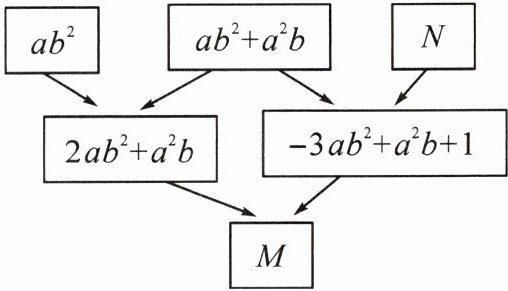
(1) 请分别求出代数式$M$，$N$；
(2) 若$a$，$b$满足$\vert a - 3\vert+(b + 1)^{2}=0$，请求出$M$的值。

答案：
(1)M = 2ab² + a²b + (-3ab² + a²b + 1)=2ab² + a²b - 3ab² + a²b + 1=-ab² + 2a²b + 1。N = -3ab² + a²b + 1 - (ab² + a²b)= -3ab² + a²b + 1 - ab² - a²b=-4ab² + 1。
(2)
∵a,b满足|a - 3| + (b + 1)² = 0，
∴a - 3 = 0,b + 1 = 0。
∴a = 3,b = -1。
∴M = -ab² + 2a²b + 1=-3×(-1)² + 2×3²×(-1) + 1=-3 + (-18) + 1=-20。

6. 有一个数学游戏，如下图，一个数从$A$，$B$，$C$三个位置中任选一个位置出发，按照通道内标注的要求进行运算后到下一个位置。例如：将$3$按照$B→C$（或$C→B$）的顺序进行运算，是将数$3$经过“乘以$-2$”的运算得出结果$-6$。

(1) 将$-2$按照$A→B→C→A$的顺序进行运算，列出算式并求出运算结果；
(2) 小明发现，将一个数按照$A→C→B→A$的顺序进行第一次运算得到的结果比这个数按照$A→B→C→A$的顺序进行第二次运算得到的结果永远大$12$，请验证这个结论。

答案：
(1)根据题意，得(-2 + 1)×(-2) - 3 = 2 - 3 = -1。
(2)设A表示的数为x，根据题意可得，第一次运算的结果为(x - 3)×(-2) + 1 = -2x + 7，第二次运算的结果为(x + 1)×(-2) - 3 = -2x - 5。
∵-2x + 7 - (-2x - 5)= -2x + 7 + 2x + 5 = 12，
∴结论正确。