《2025年名校课堂七年级数学上册华师大版河南专版》

10. 在数轴上 $-5.1$ 和 $4.9$ 之间的所有整数之和是-5.

答案： 10.-5

11. 有一组数：$1$，$-2$，$3$，$-4$，$5$，$-6$，$\cdots$，$99$，$-100$，则这 $100$ 个数的和等于-50.

答案： 11.-50

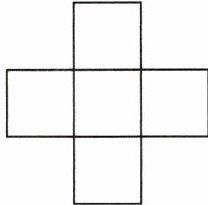
12. (2024·陕西)小华探究“幻方”时，提出了一个问题：如图，将 $0$，$-2$，$-1$，$1$，$2$ 这五个数分别填在五个小正方形内，使横向三个数之和与纵向三个数之和相等，则填入中间位置的小正方形内的数可以是0.(写出一个即可)

答案： 12.0(或2或-2)

13. 计算：
(1)$0.36 + (-7.4) + 0.5 + 0.24 + (-0.6)$；
(2)$(-2\frac{3}{5}) + (+3\frac{1}{4}) + (-3\frac{2}{5}) + |-2\frac{3}{4}| + (-1\frac{1}{2}) + |-1\frac{1}{3}|$.

答案： 13.解：
(1)原式=(0.36+0.5+0.24)+[(-7.4)+(-0.6)]=1.1+(-8)=-6.9.
(2)原式$=[(-2\frac{3}{5})+(-3\frac{2}{5})]+[(+3\frac{1}{4})+\mid-2\frac{3}{4}\mid]+[(-1\frac{1}{2})+\mid-1\frac{1}{3}\mid]=(-6)+6+(-\frac{1}{6})=-\frac{1}{6}.$

14. 一天上午，一辆警车从 $M$ 车站出发，在一条东西走向的笔直的公路上来回巡逻，行驶的路程情况如下（向东行驶记为正，向西行驶记为负，单位：$km$）.
$-7$，$+4$，$+8$，$-3$，$+10$，$-3$，$-6$，$-12$，$+9$，$-3$.
(1)这辆警车在完成上述巡逻任务后在 $M$ 车站的哪个方向，距离 $M$ 车站多少千米？
(2)若这辆警车每行驶 $100km$ 的耗油量为 $11L$，则这天上午共消耗汽油多少升？

答案： 14.解：
(1)(-7)+4+8+(-3)+10+(-3)+(-6)+(-12)+9+(-3)=[(-7)+(-3)+(-3)+(-6)+(-12)+(-3)]+(4+8+10+9)=-34+31=-3(km).故这辆警车在完成上述巡逻任务后在M车站的西边，距离M车站$3km.(2)\mid-7\mid+\mid+4\mid+\mid+8\mid+\mid-3\mid+\mid+10\mid+\mid-3\mid+\mid-6\mid+\mid-12\mid+\mid+9\mid+\mid-3\mid=7+4+8+3+10+3+6+12+9+3=65(km).65×\frac{11}{100}=7.15(L).$答：这天上午共消耗汽油7.15L.

15. 【特例呈现】对于 $(-5\frac{5}{6}) + (-9\frac{2}{3}) + 17\frac{3}{4} + (-3\frac{1}{2})$，可以按如下方法进行计算：
原式$=[(-5) + (-\frac{5}{6})] + [(-9) + (-\frac{2}{3})] + (17 + \frac{3}{4}) + [(-3) + (-\frac{1}{2})]$
$=[(-5) + (-9) + 17 + (-3)] + [(-\frac{5}{6}) + (-\frac{2}{3}) + \frac{3}{4} + (-\frac{1}{2})]$
$= 0 + (-\frac{5}{4})$
$= -\frac{5}{4}$.
【方法分析】上面这种方法叫做拆分法. 在运用拆分法将带分数拆成整数和真分数的和时，拆得的整数与真分数的符号要与原带分数的符号相同.
【方法应用】请仿照上面的方法计算：
$(-2024\frac{3}{7}) + (-2\frac{1}{4}) + (-2022\frac{2}{5}) + 4044\frac{2}{5}$.

答案： 15.解：原式$=[(-2024)+(-\frac{3}{7})]+[(-2)+(-\frac{1}{4})]+[(-2022)+(-\frac{2}{5})]+(4044+\frac{2}{5})=[(-2024)+(-2)+(-2022)+4044]+[(-\frac{3}{7})+(-\frac{1}{4})+(-\frac{2}{5})+\frac{2}{5}]=-4+(-\frac{3}{7})+(-\frac{1}{4})=-4\frac{19}{28}.$