第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
10. (2024·洛阳洛龙区期中) 下列图形中,$ \angle 1 $ 与 $ \angle 2 $ 是同位角的有(
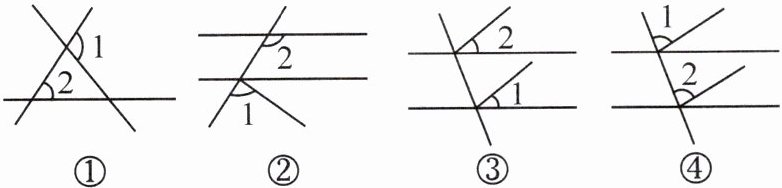
A.②③④
B.①②④
C.②③
D.③④
B
)
A.②③④
B.①②④
C.②③
D.③④
答案:
B
11. (新考向 真实情境) 风筝是中国古代劳动人民发明于春秋时期的产物,其材质在不断改进之后,坊间开始用纸做风筝,称为“纸鸢”. 在如图所示的“纸鸢”骨架示意图中,与 $ \angle 1 $ 构成内错角的是(

A.$ \angle 2 $
B.$ \angle 3 $
C.$ \angle 4 $
D.$ \angle 5 $
C
)
A.$ \angle 2 $
B.$ \angle 3 $
C.$ \angle 4 $
D.$ \angle 5 $
答案:
C
12. 如图,下列结论:① $ \angle 2 $ 与 $ \angle 3 $ 是内错角;② $ \angle 2 $ 与 $ \angle B $ 是同位角;③ $ \angle A $ 与 $ \angle B $ 是同旁内角;④ $ \angle A $ 与 $ \angle ACB $ 不是同旁内角. 其中正确的是
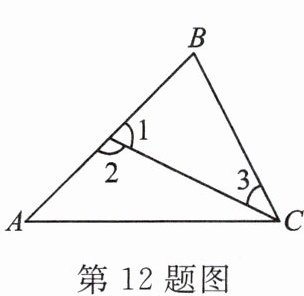
①②③
(填序号).
答案:
①②③
13. 两条直线都与第三条直线相交,$ \angle 1 $ 和 $ \angle 2 $ 是内错角,$ \angle 1 $ 和 $ \angle 3 $ 是同旁内角.
(1) 根据上述条件,画出符合题意的图形;
(2) 若 $ \angle 1 : \angle 2 : \angle 3 = 1 : 2 : 3 $,求 $ \angle 1 $,$ \angle 2 $,$ \angle 3 $ 的度数.
(1) 根据上述条件,画出符合题意的图形;
(2) 若 $ \angle 1 : \angle 2 : \angle 3 = 1 : 2 : 3 $,求 $ \angle 1 $,$ \angle 2 $,$ \angle 3 $ 的度数.
答案:
解:
(1)如图.
(2)
∵∠1:∠2:∠3=1:2:3,
∴设∠1=x°,∠2=2x°,∠3=3x°.
∵∠2与∠3是邻补角,
∴2x+3x=180,解得x=36.
∴2x=72,3x=108.
∴∠1=36°,∠2=72°,∠3=108°.

解:
(1)如图.
(2)
∵∠1:∠2:∠3=1:2:3,
∴设∠1=x°,∠2=2x°,∠3=3x°.
∵∠2与∠3是邻补角,
∴2x+3x=180,解得x=36.
∴2x=72,3x=108.
∴∠1=36°,∠2=72°,∠3=108°.

14. (新考向 推理能力) 观察图 1~图 4,回答下列问题.
(1) 请写出图 1、图 2、图 3 和图 4 中分别有几对同旁内角?
(2) 观察图形,请写出图 $ n $($ n $ 是正整数)中有几对同旁内角?
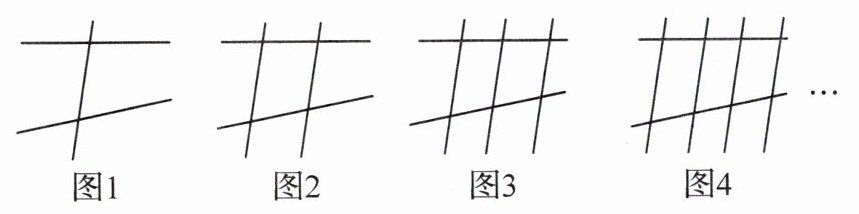
(1) 请写出图 1、图 2、图 3 和图 4 中分别有几对同旁内角?
(2) 观察图形,请写出图 $ n $($ n $ 是正整数)中有几对同旁内角?

答案:
解:
(1)图1中有2对同旁内角,图2中有8对同旁内角,图3中有18对同旁内角,图4中有32对同旁内角.
(2)图n(n是正整数)中有2n²对同旁内角.
(1)图1中有2对同旁内角,图2中有8对同旁内角,图3中有18对同旁内角,图4中有32对同旁内角.
(2)图n(n是正整数)中有2n²对同旁内角.
15. 如图,这是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动后,到达终点角. 跳动时,每一步只能跳到它的同位角、内错角或同旁内角的位置上. 如从起始位置 $ \angle 1 $ 跳到终点位置 $ \angle 3 $ 的路径有:
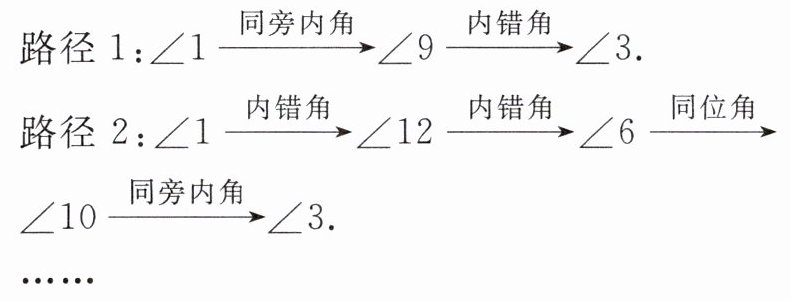
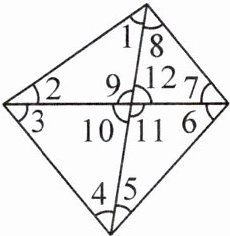
(1) 写出从 $ \angle 1 $ 到 $ \angle 8 $ 的一条路径;
(2) 从起始位置 $ \angle 1 $ 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置 $ \angle 8 $?
(3) 写出从起始位置 $ \angle 1 $ 跳到终点位置 $ \angle 8 $ 的路径,要求跳遍所有的角,且不能重复.


(1) 写出从 $ \angle 1 $ 到 $ \angle 8 $ 的一条路径;
(2) 从起始位置 $ \angle 1 $ 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置 $ \angle 8 $?
(3) 写出从起始位置 $ \angle 1 $ 跳到终点位置 $ \angle 8 $ 的路径,要求跳遍所有的角,且不能重复.
答案:
解:
(1)∠1同旁内角∠9内错角∠8(答案不唯一).
(2)能.∠1 同位角∠10内错角∠5同旁内角∠8.
(3)∠1同旁内角∠9 内错角∠10同旁内角∠3同旁内角∠4内错角∠11 同旁内角∠6内错角∠12同旁内角∠7同旁内角∠8 (答案不唯一).
(1)∠1同旁内角∠9内错角∠8(答案不唯一).
(2)能.∠1 同位角∠10内错角∠5同旁内角∠8.
(3)∠1同旁内角∠9 内错角∠10同旁内角∠3同旁内角∠4内错角∠11 同旁内角∠6内错角∠12同旁内角∠7同旁内角∠8 (答案不唯一).
查看更多完整答案,请扫码查看


