第97页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. 如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP= 20,cosα= $\frac{4}{5}$,则点P的坐标为(
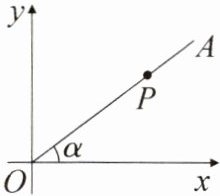
A.(16,20)
B.(16,12)
C.(20,16)
D.(12,16)
B
)
A.(16,20)
B.(16,12)
C.(20,16)
D.(12,16)
答案:
B
13. [转化思想]如图,在△ABC中,∠ACB= 90°,D为AB的中点,连接CD。若BC= 4,CD= 3,则cos∠DCB的值为
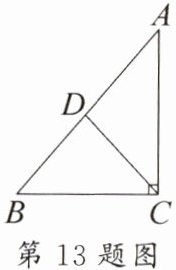
$\frac{2}{3}$
。
答案:
$\frac{2}{3}$
14. [T4变式]如图,△ABC的三个顶点均在正方形网格的格点上,则cosA的值为
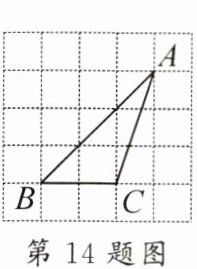
$\frac{2\sqrt{5}}{5}$
。
答案:
$\frac{2\sqrt{5}}{5}$
15. 如图,在△ABC中,AB= 10,cos∠ABC= $\frac{3}{5}$,D为BC边上一点,且AD= AC。若CD= 4,求BD的长。
]
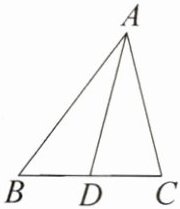
]

答案:
4
16. 新考向 阅读理解 阅读下面的材料,先填空,再按要求答题。
sin30°= $\frac{1}{2}$,cos30°= $\frac{\sqrt{3}}{2}$,则sin^230°+cos^230°=
sin45°= $\frac{\sqrt{2}}{2}$,cos45°= $\frac{\sqrt{2}}{2}$,则sin^245°+cos^245°=
sin60°= $\frac{\sqrt{3}}{2}$,cos60°= $\frac{1}{2}$,则sin^260°+cos^260°=
……
观察上述式子,猜想:对于任意锐角A,都有sin^2A+cos^2A=
(1)如图,在锐角三角形ABC中,利用三角函数的概念及勾股定理证明上述猜想;
(2)已知∠A为锐角,且sinA= $\frac{3}{5}$,求cosA的值。
]
sin30°= $\frac{1}{2}$,cos30°= $\frac{\sqrt{3}}{2}$,则sin^230°+cos^230°=
1
;sin45°= $\frac{\sqrt{2}}{2}$,cos45°= $\frac{\sqrt{2}}{2}$,则sin^245°+cos^245°=
1
;sin60°= $\frac{\sqrt{3}}{2}$,cos60°= $\frac{1}{2}$,则sin^260°+cos^260°=
1
;……
观察上述式子,猜想:对于任意锐角A,都有sin^2A+cos^2A=
1
。(1)如图,在锐角三角形ABC中,利用三角函数的概念及勾股定理证明上述猜想;
(2)已知∠A为锐角,且sinA= $\frac{3}{5}$,求cosA的值。
]

答案:
1 1 1 1
(1)证明:如图,过点B作$BH\perp AC$于点H,则在$Rt\triangle ABH$中,$BH^{2}+AH^{2}=AB^{2}$,$\sin A=\frac{BH}{AB}$,$\cos A=\frac{AH}{AB}$,$\therefore \sin^{2}A+\cos^{2}A=\frac{BH^{2}}{AB^{2}}+\frac{AH^{2}}{AB^{2}}=\frac{BH^{2}+AH^{2}}{AB^{2}}=\frac{AB^{2}}{AB^{2}}=1$.
(2)解:$\because \sin^{2}A+\cos^{2}A=1$,$\sin A=\frac{3}{5}$,$\therefore \cos^{2}A=1-\left(\frac{3}{5}\right)^{2}=\frac{16}{25}$.又$\cos A>0$,$\therefore \cos A=\frac{4}{5}$.
(1)证明:如图,过点B作$BH\perp AC$于点H,则在$Rt\triangle ABH$中,$BH^{2}+AH^{2}=AB^{2}$,$\sin A=\frac{BH}{AB}$,$\cos A=\frac{AH}{AB}$,$\therefore \sin^{2}A+\cos^{2}A=\frac{BH^{2}}{AB^{2}}+\frac{AH^{2}}{AB^{2}}=\frac{BH^{2}+AH^{2}}{AB^{2}}=\frac{AB^{2}}{AB^{2}}=1$.
(2)解:$\because \sin^{2}A+\cos^{2}A=1$,$\sin A=\frac{3}{5}$,$\therefore \cos^{2}A=1-\left(\frac{3}{5}\right)^{2}=\frac{16}{25}$.又$\cos A>0$,$\therefore \cos A=\frac{4}{5}$.
查看更多完整答案,请扫码查看


