《2025年状元成才路创优作业九年级数学上册湘教版》

9. [2025·永州道县期中]若$y= (m + 2)x^{\vert m\vert - 3}$是关于x的反比例函数,则$m$的值为2。

答案： 2

10. 给出六个关系式：
①$x(y + 1)= 5$；②$y= \frac{2}{x + 2}$；③$y= \frac{1}{x^{2}}$；
④$y= -\frac{1}{2x}$；⑤$y= -\frac{x}{2\pi}$；⑥$xy= \frac{2}{3}$。
其中$y是x$的反比例函数的是(D)
A.①②③④⑥
B.③⑤⑥
C.④⑤⑥
D.④⑥

答案： D

11. 下列函数关系中,是反比例函数的是(D)
A.圆的面积$S与半径R$的关系
B.直角三角形两锐角$A与B$的关系
C.等腰三角形的顶角$A与底角B$的关系
D.面积为$20的菱形的两条对角线y与x$的关系

答案： D

12. 新考向 跨物理·杠杆原理 阿基米德说：“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“动力$×动力臂= 阻力×$阻力臂”。如图,小明想要用撬棍撬动一块大石头,已知阻力为$1200N$,阻力臂长为$0.5m$。设动力为$y$($N$),动力臂长为$x$($m$)。(图中撬棍本身所受的重力忽略不计)
(1)求$y关于x$的函数表达式；

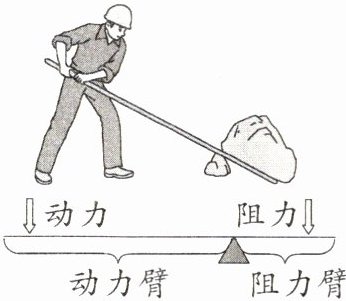
(2)当动力臂长为$1.5m$时,撬动石头至少需要多大的力？

答案：
(1)$y=\frac{600}{x}$.
(2)400 N.

13. 已知$y = y_{1}+y_{2}$,$y_{1}与x - 1$成正比例,$y_{2}与x + 1$成反比例,并且当$x = 0$时,$y = - 3$；当$x = 1$时,$y = - 1$。
(1)求$y关于x$的函数表达式；
(2)当$x= -\frac{1}{2}$时,求$y$的值。

答案：
(1)$y=x-1-\frac{2}{x+1}$.
(2)$-\frac{11}{2}$.

14. [新定义问题]定义：形如$f(x)= ax+\frac{b}{x}(ab\gt0)$的函数为“双飞燕函数”.若函数$f(x)= (k - 1)x - x^{k^{2}-3}$是“双飞燕函数”,则$k$的值为$-\sqrt{2}$。

答案： $-\sqrt{2}$