第83页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. 如图,在方格纸中,以点 $ O $ 为位似中心,将 $\triangle ABC$ 缩小为原图形的 $\frac{1}{2}$,则点 $ A $ 的对应点为(
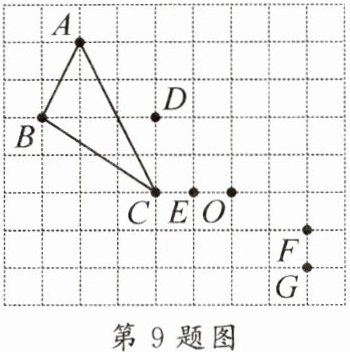
A.点 $ D $
B.点 $ E $
C.点 $ D $ 或点 $ F $
D.点 $ D $ 或点 $ G $
D
)
A.点 $ D $
B.点 $ E $
C.点 $ D $ 或点 $ F $
D.点 $ D $ 或点 $ G $
答案:
D
10. 新考向 情境题·投影仪 如图,投影仪在放映时,其原理可以看作是将胶片上的画面放大并投影到荧幕上。已知镜头到胶片的距离为 $ 0.25 $ m,镜头到荧幕的距离为 $ 5 $ m,且投影的画面正好铺满整个荧幕,则胶片与荧幕的面积比为
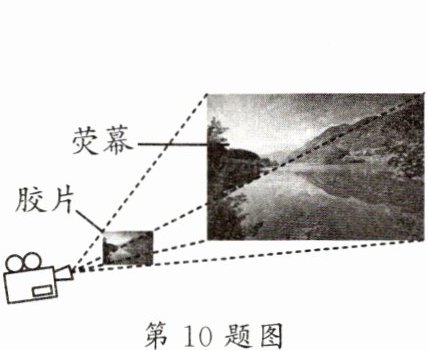
1:400
。
答案:
1:400
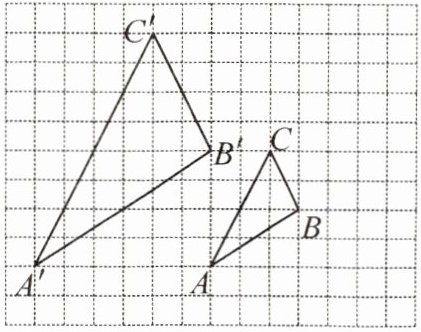
11. 如图,每个小方格都是边长为 1 的正方形,$\triangle ABC$ 与 $\triangle A'B'C'$ 是以点 $ O $ 为位似中心的位似图形,它们的顶点都在小正方形的顶点上。
(1)画出点 $ O $,并求出 $\triangle ABC$ 与 $\triangle A'B'C'$ 的位似比;
(2)以点 $ O $ 为位似中心,在网格图中将 $\triangle ABC$ 放大为原图形的 1.5 倍,画出所得的 $\triangle A_1B_1C_1$。
(1)画出点 $ O $,并求出 $\triangle ABC$ 与 $\triangle A'B'C'$ 的位似比;
(2)以点 $ O $ 为位似中心,在网格图中将 $\triangle ABC$ 放大为原图形的 1.5 倍,画出所得的 $\triangle A_1B_1C_1$。

答案:
(1)图略.位似比为$\frac{1}{2}$.
(2)略.
(1)图略.位似比为$\frac{1}{2}$.
(2)略.
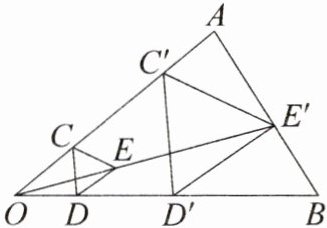
12. 如图,用下面的方法可以画 $\triangle AOB$ 的内接等边三角形,阅读后证明相应问题。
作法:
①在 $\triangle AOB$ 内画等边三角形 $ CDE $,使点 $ C $ 在 $ OA $ 上,点 $ D $ 在 $ OB $ 上;
②连接 $ OE $ 并延长,交 $ AB $ 于点 $ E' $,过点 $ E' $ 作 $ E'C' // EC $,交 $ OA $ 于点 $ C' $,作 $ E'D' // ED $,交 $ OB $ 于点 $ D' $;
③连接 $ C'D' $,则 $\triangle C'D'E'$ 是 $\triangle AOB$ 的内接等边三角形。
求证:$\triangle C'D'E'$ 是等边三角形。
作法:
①在 $\triangle AOB$ 内画等边三角形 $ CDE $,使点 $ C $ 在 $ OA $ 上,点 $ D $ 在 $ OB $ 上;
②连接 $ OE $ 并延长,交 $ AB $ 于点 $ E' $,过点 $ E' $ 作 $ E'C' // EC $,交 $ OA $ 于点 $ C' $,作 $ E'D' // ED $,交 $ OB $ 于点 $ D' $;
③连接 $ C'D' $,则 $\triangle C'D'E'$ 是 $\triangle AOB$ 的内接等边三角形。
求证:$\triangle C'D'E'$ 是等边三角形。

答案:
证明:
∵E'C'//EC,E'D'//ED,
∴△OCE∽△OC'E',△ODE∽△OD'E'.
∴$\frac{CE}{C'E'}=\frac{OE}{OE'}$,$\frac{DE}{D'E'}=\frac{OE}{OE'}$,∠CEO=∠C'E'O,∠DEO=∠D'E'O.
∴$\frac{CE}{C'E'}=\frac{DE}{D'E'}$,∠CED=∠C'E'D'.
∴△CDE∽△C'D'E'.
∵△CDE 是等边三角形,
∴△C'D'E'是等边三角形.
∵E'C'//EC,E'D'//ED,
∴△OCE∽△OC'E',△ODE∽△OD'E'.
∴$\frac{CE}{C'E'}=\frac{OE}{OE'}$,$\frac{DE}{D'E'}=\frac{OE}{OE'}$,∠CEO=∠C'E'O,∠DEO=∠D'E'O.
∴$\frac{CE}{C'E'}=\frac{DE}{D'E'}$,∠CED=∠C'E'D'.
∴△CDE∽△C'D'E'.
∵△CDE 是等边三角形,
∴△C'D'E'是等边三角形.
查看更多完整答案,请扫码查看


