第65页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. 新考向 尺规作图 在数学课上,老师布置了一道题,要求同学们利用尺规作图使△ADE与△ABC相似,下面是小华和小亮所作的图形:
 关于小华和小亮的作法,下列判断正确的是(
关于小华和小亮的作法,下列判断正确的是(
A.小华对,小亮错
B.小华错,小亮对
C.两个人都对
D.两个人都错
 关于小华和小亮的作法,下列判断正确的是(
关于小华和小亮的作法,下列判断正确的是(C
)A.小华对,小亮错
B.小华错,小亮对
C.两个人都对
D.两个人都错
答案:
C
10. 如图,在△ABC中,AD是中线,BC= 8,∠B= ∠DAC,则线段AC的长为(
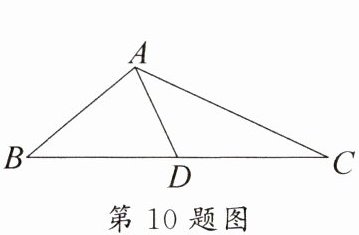
A.4
$B.4√{2} $
C.6
$D.4√{3}$
B
)
A.4
$B.4√{2} $
C.6
$D.4√{3}$
答案:
B
11. 如图,在菱形ABCD中,点M,N在AC上,ME⊥AD于点E,NF⊥AB于点F.若NF= NM= 2,ME= 3,则AN的长为
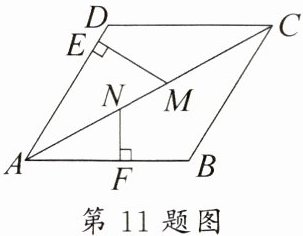
4
.
答案:
4
12. 如图,在□ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,连接AF,且∠AFE= ∠B.
(1)求证:△ADF∽△DEC;
(2)若AB= 4,BC= 3√{3},AF= 2√{3},求AE的长.
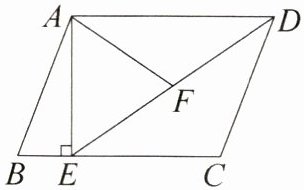
(1)求证:△ADF∽△DEC;
(2)若AB= 4,BC= 3√{3},AF= 2√{3},求AE的长.

答案:
(1)略.
(2)3.
(1)略.
(2)3.
13. 新考向 类比探究 (1)如图①,在四边形ABCD中,P为AB上一点,∠DPC= ∠A= ∠B= 90°,求证:AD·BC= AP·BP.
(2)如图②,在四边形ABCD中,P为AB上一点,当∠DPC= ∠A= ∠B时,(1)中的结论是否依然成立?请说明理由.

(2)如图②,在四边形ABCD中,P为AB上一点,当∠DPC= ∠A= ∠B时,(1)中的结论是否依然成立?请说明理由.

答案:
(1)证明:
∵∠DPC=∠A=90°,
∴∠ADP+∠APD=90°,∠BPC+∠APD=180°-∠DPC=90°.
∴∠ADP=∠BPC.又∠A=∠B,
∴△ADP∽△BPC.
∴$\frac{AD}{BP}=\frac{AP}{BC}$.
∴AD·BC=AP·BP.
(2)解:
(1)中的结论 AD·BC=AP·BP 依然成立.理由如下:
∵∠BPD=∠DPC+∠BPC=∠A+∠ADP,且∠DPC=∠A,
∴∠ADP=∠BPC.又∠A=∠B,
∴△ADP∽△BPC.
∴$\frac{AD}{BP}=\frac{AP}{BC}$.
∴AD·BC=AP·BP.
(1)证明:
∵∠DPC=∠A=90°,
∴∠ADP+∠APD=90°,∠BPC+∠APD=180°-∠DPC=90°.
∴∠ADP=∠BPC.又∠A=∠B,
∴△ADP∽△BPC.
∴$\frac{AD}{BP}=\frac{AP}{BC}$.
∴AD·BC=AP·BP.
(2)解:
(1)中的结论 AD·BC=AP·BP 依然成立.理由如下:
∵∠BPD=∠DPC+∠BPC=∠A+∠ADP,且∠DPC=∠A,
∴∠ADP=∠BPC.又∠A=∠B,
∴△ADP∽△BPC.
∴$\frac{AD}{BP}=\frac{AP}{BC}$.
∴AD·BC=AP·BP.
查看更多完整答案,请扫码查看


