第7页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 已知反比例函数 $ y = \frac{k}{x} (k \neq 0) $,且在每个象限内,函数值 $ y $ 随自变量 $ x $ 的增大而增大,则下列各点可能在这个函数图象上的是 (
A.$ (2, 3) $
B.$ (-2, 3) $
C.$ (3, 0) $
D.$ (-3, 0) $
B
)A.$ (2, 3) $
B.$ (-2, 3) $
C.$ (3, 0) $
D.$ (-3, 0) $
答案:
B
9. [T6 变式][2025·武冈期中]已知点 $ A(-2, y_1) $,$ B(-1, y_2) $,$ C(3, y_3) $ 在反比例函数 $ y = \frac{k}{x} (k < 0) $ 的图象上,则 $ y_1 $,$ y_2 $,$ y_3 $ 的大小关系是 (
A.$ y_1 < y_2 < y_3 $
B.$ y_2 < y_1 < y_3 $
C.$ y_3 < y_1 < y_2 $
D.$ y_3 < y_2 < y_1 $
C
)A.$ y_1 < y_2 < y_3 $
B.$ y_2 < y_1 < y_3 $
C.$ y_3 < y_1 < y_2 $
D.$ y_3 < y_2 < y_1 $
答案:
C
10. 如图是三个反比例函数 $ y_1 = \frac{k_1}{x} $,$ y_2 = \frac{k_2}{x} $,$ y_3 = \frac{k_3}{x} $ 在 $ x $ 轴上方的图象,则 $ k_1 $,$ k_2 $,$ k_3 $ 的大小关系为
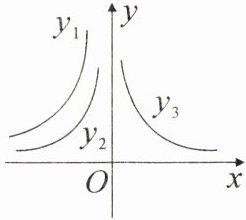
k₁<k₂<k₃
(用“$ < $”连接)。
答案:
k₁<k₂<k₃
11. [教材 P13 习题 T6 变式题]如图,点 $ A(-2, n) $ 在反比例函数 $ y = \frac{m - 3}{x} (x < 0) $ 的图象上,作 $ AB \perp x $ 轴,垂足为点 $ B $,连接 $ OA $,$ OA = 2\sqrt{2} $。
(1)求 $ m $ 的值;
(2)若点 $ C(a, y_1) $,$ D(a + 2, y_2) (a > 0) $ 在这个函数的图象上,试比较 $ y_1 $ 与 $ y_2 $ 的大小。
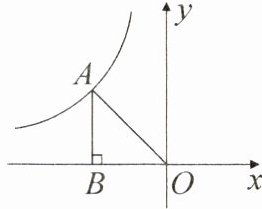
(1)求 $ m $ 的值;
(2)若点 $ C(a, y_1) $,$ D(a + 2, y_2) (a > 0) $ 在这个函数的图象上,试比较 $ y_1 $ 与 $ y_2 $ 的大小。

答案:
解:
(1)因为AB⊥x轴,所以∠ABO = 90°.
因为点A(−2,n),OA = 2$\sqrt{2}$,
所以在Rt△ABO中,由勾股定理,得2² + n² = (2$\sqrt{2}$)²,
解得n₁ = 2,n₂ = −2(不合题意,舍去).
故点A的坐标为(−2,2).
又点A在反比例函数y = $\frac{m - 3}{x}$的图象上,
所以2 = $\frac{m - 3}{-2}$,所以m = −1.
(2)由m = −1可得反比例函数的表达式是y = −$\frac{4}{x}$.
所以该函数的图象位于第二、四象限,且在每一象限内,函数值y随自变量x的增大而增大.
因为点C(a,y₁),D(a + 2,y₂)(a>0)在反比例函数y = −$\frac{4}{x}$的图象上,且a + 2>a>0,所以y₁<y₂.
(1)因为AB⊥x轴,所以∠ABO = 90°.
因为点A(−2,n),OA = 2$\sqrt{2}$,
所以在Rt△ABO中,由勾股定理,得2² + n² = (2$\sqrt{2}$)²,
解得n₁ = 2,n₂ = −2(不合题意,舍去).
故点A的坐标为(−2,2).
又点A在反比例函数y = $\frac{m - 3}{x}$的图象上,
所以2 = $\frac{m - 3}{-2}$,所以m = −1.
(2)由m = −1可得反比例函数的表达式是y = −$\frac{4}{x}$.
所以该函数的图象位于第二、四象限,且在每一象限内,函数值y随自变量x的增大而增大.
因为点C(a,y₁),D(a + 2,y₂)(a>0)在反比例函数y = −$\frac{4}{x}$的图象上,且a + 2>a>0,所以y₁<y₂.
12. 新考向 探究性试题 小明在学习了反比例函数的图象与性质后,进一步探究了函数 $ y = -\frac{1}{|x|} $ 的图象与性质。其探究过程如下:
(1)画出函数图象。
①列表:下表是 $ x $ 与 $ y $ 的几组对应值,其中 $ m = $______;
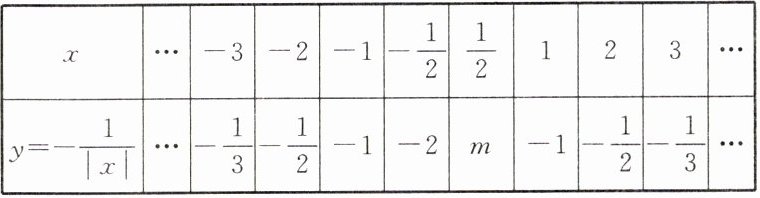
②描点:在如图所示的平面直角坐标系中,根据表中各组对应值,描出相应的点;
③连线:把 $ y $ 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,图中已画出了部分图象,请你把图象补充完整。

(2)通过观察图象,写出该函数的两条性质。
(1)画出函数图象。
①列表:下表是 $ x $ 与 $ y $ 的几组对应值,其中 $ m = $______;

②描点:在如图所示的平面直角坐标系中,根据表中各组对应值,描出相应的点;
③连线:把 $ y $ 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,图中已画出了部分图象,请你把图象补充完整。

(2)通过观察图象,写出该函数的两条性质。
答案:
解:
(1)①−2
②③如图所示.
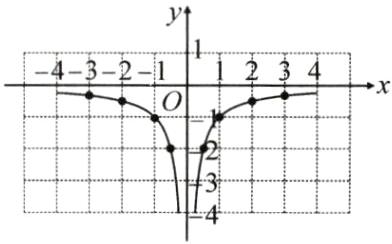
(2)该函数有如下性质:
①图象关于y轴对称;
②当x<0时,函数值y随自变量x的增大而减小;当x>0时,函数值y随自变量x的增大而增大.(答案不唯一)
解:
(1)①−2
②③如图所示.

(2)该函数有如下性质:
①图象关于y轴对称;
②当x<0时,函数值y随自变量x的增大而减小;当x>0时,函数值y随自变量x的增大而增大.(答案不唯一)
查看更多完整答案,请扫码查看


