《2025年状元成才路创优作业九年级数学上册湘教版》

10. 若关于 $x$ 的方程 $(m + 2)x^{\vert m\vert} - mx + 2 = 0$ 是一元二次方程,则 $m = $2.

答案： 2

变式题 [易错变式]若关于 $x$ 的一元二次方程 $(m - 3)x^{2} + 5x + \vert m\vert - 3 = 0$ 的常数项为 $0$,则 $m$ 的值为-3.

答案： -3

11. 在方程①$2x - 3y + 1 = 0$,②$x(4x - 2) = 0$,③$x + 3 = \frac{1}{x}$,④$x^{2} + 3x = 5$,⑤$ax^{2} + 2x + 1 = 0$,⑥$x^{2} + 3x = (x + 1)^{2}$ 中,一定是一元二次方程的个数是 (B)
A.$1$
B.$2$
C.$3$
D.$4$

答案： B

12. 新考向 数学文化·古算题 我国古代数学著作《九章算术》中有这样一个问题：“今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何.”其大意是：“已知矩形门的高比宽多 $6$ 尺 $8$ 寸 ($1$ 尺 $= 10$ 寸),门的对角线长 $1$ 丈 ($1$ 丈 $= 10$ 尺),那么门的高和宽各是多少？”若设门的宽为 $x$ 尺,则可列方程为 (D)
A.$x(x + 6.8) = 10^{2}$
B.$x^{2} + (x - 6.8)^{2} = 10^{2}$
C.$x(x - 6.8) = 10^{2}$
D.$x^{2} + (x + 6.8)^{2} = 10^{2}$

答案： D

13. 将关于 $x$ 的一元二次方程 $2x^{2} - 3x = ax(x - 1) + 1$ 化为二次项系数为 $1$ 的一般形式后,若其常数项为 $- 1$,则一次项系数为-2.

答案： -2

14. 已知关于 $x$ 的方程 $(k^{2} - 1)x^{2} + (k + 1)x - 2 = 0$.
(1)当 $k$ 取何值时,此方程为一元一次方程？求出此方程的解.
(2)当 $k$ 取何值时,此方程为一元二次方程？写出这个一元二次方程的二次项系数、一次项系数和常数项.

答案：
(1)k=1,此方程的解为x=1.
(2)k≠±1,二次项系数是k²-1,一次项系数是k+1,常数项是-2.

15. 根据题意,列出关于 $x$ 的方程：
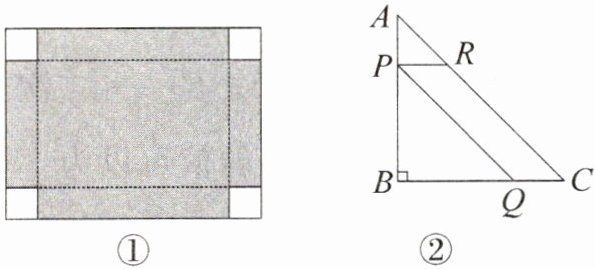
(1)[教材 P29 习题 T6 变式题]如图①,在一块长为 $40$ cm、宽为 $30$ cm 的矩形纸板的四个角各剪去一个边长为 $x$ cm 的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒,该无盖纸盒的底面积为 $600$ $cm^{2}$.
(2)如图②,在 $Rt\triangle ABC$ 中,$\angle B = 90^{\circ}$,$AB = BC = 8$ cm,动点 $P$ 从点 $A$ 出发沿 $AB$ 向点 $B$ 移动,过点 $P$ 分别作 $PQ// AC$ 交 $BC$ 于点 $Q$,$PR// BC$ 交 $AC$ 于点 $R$.当 $AP$ 的长为多少时,四边形 $PQCR$ 的面积为 $16$ $cm^{2}$？设 $AP$ 的长为 $x$ cm.

答案：
(1)(40-2x)(30-2x)=600.
(2)x(8-x)=16.