第44页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图,某小区中央花园有一块长方形花圃,它的长为 $ x $ m,宽为 $ 5 $ m。若长不变,将宽扩大,使得扩大后的花圃变成正方形,且面积比原来增加 $ 15 $ m^2,则可列方程为(
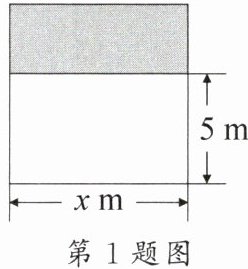
A.$ x(x + 5) = 15 $
B.$ x(x - 5) = 15 $
C.$ (x - 5)^2 = 15 $
D.$ x^2 - 5^2 = 15 $
B
)
A.$ x(x + 5) = 15 $
B.$ x(x - 5) = 15 $
C.$ (x - 5)^2 = 15 $
D.$ x^2 - 5^2 = 15 $
答案:
B
2. 一个直角三角形的两条直角边长的和是 $ 6 $ cm,面积为 $ 4 $ cm^2,则这个直角三角形较长的直角边的长为
4
cm。
答案:
4
3. 如图,某校打算用 $ 14 $ m 长的篱笆在墙边(墙足够长)围成一个矩形区域 $ ABCD $ 作为“养殖基地”(篱笆只围 $ AB $,$ BC $,$ CD $ 三边),当矩形区域的面积是 $ 24 $ m^2 时,$ BC $ 的长为
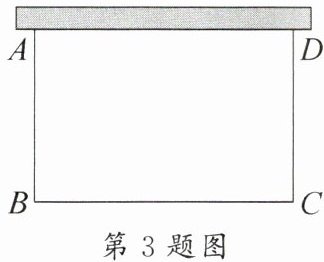
6 m 或 8 m
。
答案:
6 m 或 8 m
4. 广西壮锦被誉为指尖上的非遗,经纬交织之处,绘就民族华章。如图,在一幅长为 $ 60 $ cm、宽为 $ 40 $ cm 的广西壮锦的四周镶上等宽的锦缎边饰,制成一幅矩形挂画,如果要使整个挂画(图中虚线边框矩形)的面积是 $ 2709 $ cm^2,设锦缎边饰的宽度为 $ x $ cm,那么 $ x $ 满足的方程是(
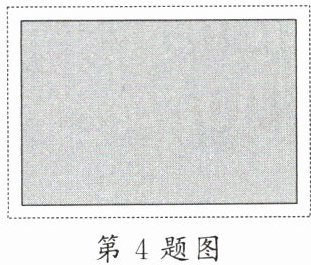
A.$ (60 + 2x)(40 + x) = 2709 $
B.$ (60 + 2x)(40 + 2x) = 2709 $
C.$ (60 + x)(40 + 2x) = 2709 $
D.$ (60 + x)(40 + x) = 2709 $
B
)
A.$ (60 + 2x)(40 + x) = 2709 $
B.$ (60 + 2x)(40 + 2x) = 2709 $
C.$ (60 + x)(40 + 2x) = 2709 $
D.$ (60 + x)(40 + x) = 2709 $
答案:
B
5. [教材 P52 练习 T1 变式题]如图,在一块长为 $ 12 $ m、宽为 $ 8 $ m 的矩形空地上修建同样宽的两条互相垂直的道路(两条道路各与矩形的一边平行),剩余部分栽种花草,且栽种花草的面积为 $ 77 $ m^2,则道路的宽为
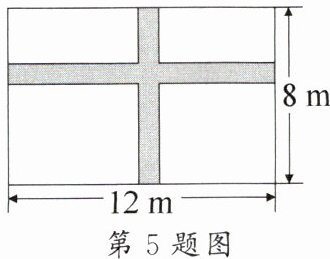
1
m。
答案:
1
6. 新考向 情境题·停车场 如图是某停车场的平面示意图,停车场外围的长为 $ 33 $ m,宽为 $ 20 $ m,停车场内车道的宽度都相等。若停车位的总占地面积为 $ 510 $ m^2,求车道的宽度。
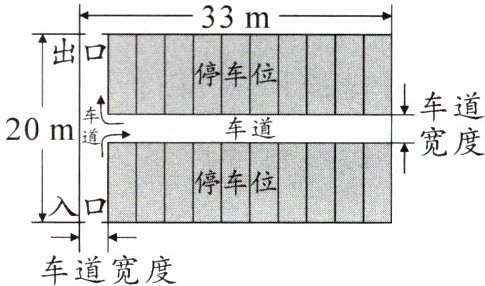

答案:
3 m.
7. [教材 P53 练习 T2 变式题]如图,在 $ Rt\triangle ABC $ 中,$ \angle B = 90° $,$ AB = 8 $ cm,$ BC = 10 $ cm,点 $ P $ 从点 $ A $ 出发,在线段 $ AB $ 上以 $ 1 $ cm/s 的速度向终点 $ B $ 运动;点 $ Q $ 从点 $ B $ 出发,在线段 $ BC $ 上以 $ 2 $ cm/s 的速度向终点 $ C $ 运动。如果点 $ P $,$ Q $ 同时出发,设动点的运动时间为 $ x $ s。
(1)$ AP = $
(2)经过几秒,$ \triangle PBQ $ 的面积为 $ 15 $ cm^2?
(1)$ AP = $
x
cm,$ BQ = $2x
cm,$ PB = $(8-x)
cm;(均用含 $ x $ 的代数式表示)(2)经过几秒,$ \triangle PBQ $ 的面积为 $ 15 $ cm^2?
经过3s或5s,△PBQ的面积为15cm²。
答案:
(1)x 2x (8-x)
(2)3 s 或 5 s.
(1)x 2x (8-x)
(2)3 s 或 5 s.
查看更多完整答案,请扫码查看


