《2025年状元成才路创优作业九年级数学上册湘教版》

1. 已知关于 $ x $ 的方程 $(k - 3)x^{|k| - 1} - 3x + 4 = 0$ 是一元二次方程,则 $ k $ 的值为(C)
A.$\pm 3$
B.$ 3 $
C.$ - 3 $
D.不能确定

答案： C

2. 若关于 $ x $ 的一元二次方程 $(m + 1)x^{2} + 2x - m^{2} + 1 = 0$ 的常数项为 $ 0 $,则 $ m $ 的值为(B)
A.$ 0 $
B.$ 1 $
C.$ - 1 $
D.$ 1 $ 或 $ - 1 $

答案： B

3. 若 $ 1 $ 是关于 $ x $ 的一元二次方程 $(m - 2)x^{2} + 4x - m^{2} = 0$ 的一个根,则 $ m $ 的值为-1。

答案： -1

4. [2025·临湘期末]若关于 $ x $ 的一元二次方程 $ kx^{2} - 2x - 1 = 0 $ 有实数根,则 $ k $ 的取值范围是k≥-1且k≠0。

答案： k≥-1且k≠0

5. 解下列方程：
(1) $ 3x^{2} + x = 5 $；
(2) $ 4x(x + 2) = 3(x + 2) $。

答案：
(1)$x_{1}=\frac{-1+\sqrt{61}}{6}$,$x_{2}=\frac{-1-\sqrt{61}}{6}$.
(2)$x_{1}=-2$,$x_{2}=\frac{3}{4}$.

6. 已知关于 $ x $ 的一元二次方程 $ x^{2} + 2mx + m^{2} + m = 0 $ 的两个根分别是 $ \alpha,\beta $,若 $ \alpha^{2} + \beta^{2} = 12 $,则 $ m $ 的值为-2。

答案： -2

7. 若关于 $ x $ 的方程 $ x^{2} + (2m - 1)x + m^{2} = 0 $ 的两个实数根为 $ x_{1},x_{2} $,且 $ x_{1} + x_{2} + x_{1}x_{2} - 1 = 0 $,求 $ m $ 的值。

答案： 0.

8. [2024·赤峰中考改编]等腰三角形的两边长分别是方程 $ x^{2} - 10x + 21 = 0 $ 的两个根,则这个三角形的周长为17。

答案： 17

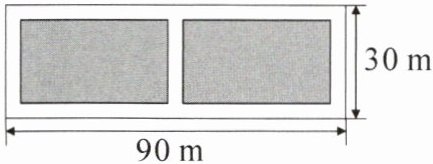
9. 如图,某农家乐老板计划将一块长为 $ 90\ m $、宽为 $ 30\ m $ 的长方形空地开挖成两块形状和大小均相同的长方形垂钓鱼塘,两块垂钓鱼塘的面积之和为 $ 1500\ m^{2} $,且它们中间及周边留有宽度相等的垂钓通道,则垂钓通道的宽度为5 m。

答案： 5 m