第75页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
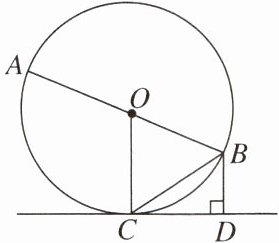
8. 如图,AB 是$\odot O$的直径,C 为$\odot O$上一点,过点 B 作$BD\perp CD$,垂足为 D,连结 BC,BC 平分$\angle ABD$.求证:CD 为$\odot O$的切线.

答案:
证明:
∵BC 平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC//BD.
∵BD⊥CD,
∴OC⊥CD,
∴CD 为$\odot O$的切线.
∵BC 平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC//BD.
∵BD⊥CD,
∴OC⊥CD,
∴CD 为$\odot O$的切线.
9. 如图,CD 是$\odot O$的直径,BD 是弦,延长 DC 到点 A,使$\angle ABD= 120°$,若添加一个条件,使 AB 是$\odot O$的切线,有下列几个条件:①$AC= BC$.②$AC= OC$.③$OC= BC$.其中能使命题成立的所有条件是( )
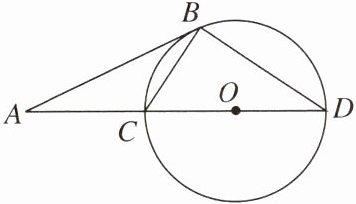
A.①②
B.①③
C.②③
D.①②③

A.①②
B.①③
C.②③
D.①②③
答案:
D
10. 如图,$\angle ABC= 80°$,O 为射线 BC 上一点,以点 O 为圆心,$\frac{1}{2}OB长为半径作\odot O$,要使射线 BA 与$\odot O$相切,应将射线 BA 绕点 B 按顺时针方向旋转______.
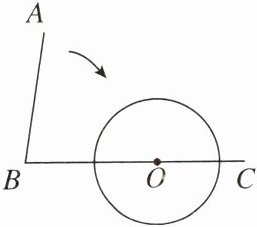

答案:
50°或 110°
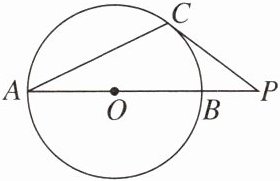
11. 如图,C 是$\odot O$上一点,点 P 在直径 AB 的延长线上,$\odot O$的半径为 3,$PB= 2$,$PC= 4$.求证:PC 是$\odot O$的切线.

答案:
证明:如图,连结 OC.
∵$\odot O$的半径为 3,
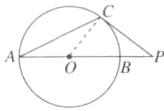
∴OC=OB=3.
又
∵BP=2,
∴OP=5.
在△OCP 中,OC²+PC²=3²+4²=5²=OP²,
∴△OCP 为直角三角形,∠OCP=90°,
∴OC⊥PC,
∴PC 是$\odot O$的切线.
证明:如图,连结 OC.
∵$\odot O$的半径为 3,

∴OC=OB=3.
又
∵BP=2,
∴OP=5.
在△OCP 中,OC²+PC²=3²+4²=5²=OP²,
∴△OCP 为直角三角形,∠OCP=90°,
∴OC⊥PC,
∴PC 是$\odot O$的切线.
12. 已知$\triangle ABC内接于\odot O$,过点 A 作直线 EF.
(1)如图 1,若 AB 为$\odot O$的直径,要使 EF 成为$\odot O$的切线,还需要添加的一个条件(要求写出两种情况):______或______.
(2)如图 2,如果 AB 是不过圆心 O 的弦,且$\angle CAE= \angle B$,那么 EF 是$\odot O$的切线吗? 试证明你的判断.
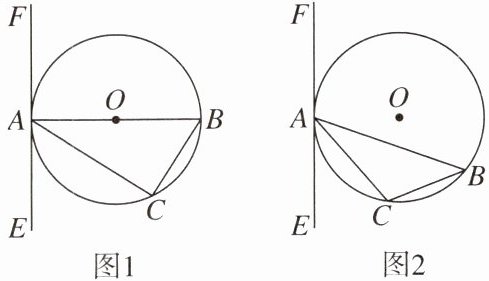
(1)如图 1,若 AB 为$\odot O$的直径,要使 EF 成为$\odot O$的切线,还需要添加的一个条件(要求写出两种情况):______或______.
(2)如图 2,如果 AB 是不过圆心 O 的弦,且$\angle CAE= \angle B$,那么 EF 是$\odot O$的切线吗? 试证明你的判断.

答案:
(1)∠BAE=90° ∠CAE=∠B
(2)EF 是$\odot O$的切线.
证明:如图,连结 AO 并延长交$\odot O$于点 M,连结 MC,则∠ACM=90°,∠M=∠B,
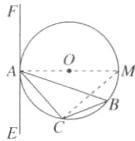
∴∠M+∠CAM=∠B+∠CAM=90°.
∵∠CAE=∠B,
∴∠CAE+∠CAM=90°,
∴AE⊥AM,
∴EF 是$\odot O$的切线.
(1)∠BAE=90° ∠CAE=∠B
(2)EF 是$\odot O$的切线.
证明:如图,连结 AO 并延长交$\odot O$于点 M,连结 MC,则∠ACM=90°,∠M=∠B,

∴∠M+∠CAM=∠B+∠CAM=90°.
∵∠CAE=∠B,
∴∠CAE+∠CAM=90°,
∴AE⊥AM,
∴EF 是$\odot O$的切线.
查看更多完整答案,请扫码查看


