《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

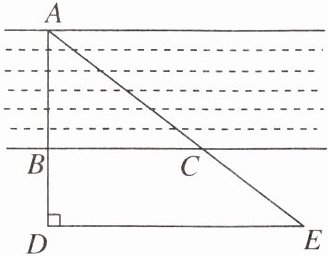
7. 为了估计河的宽度,勘测人员在河的对岸选定一个目标点 A,在近岸分别取点 B,D,E,C,使点 A,B,D 在一条直线上,点 A,C,E 也在一条直线上,且 DE//BC. 经测量,BC= 25 米,BD= 12 米,DE= 40 米,求河的宽度 AB.

答案： 解：
∵BC//DE，
∴△ABC∽△ADE，
∴$\frac{BC}{DE}=\frac{AB}{AD}$，即$\frac{25}{40}=\frac{AB}{AB+12}$，解得AB=20. 故河的宽度AB为20米.

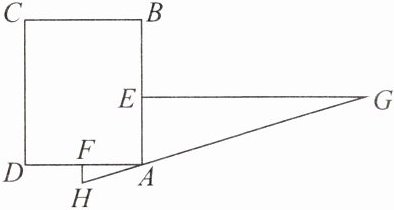
8. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问：出南门几何步而见木？”这段话摘自《九章算术》,意思是说：如图,矩形城池 ABCD,东边城墙 AB 长 9 里,南边城墙 AD 长 7 里,东门点 E、南门点 F 分别是 AB,AD 的中点,EG⊥AB,FH⊥AD,EG= 15 里,HG 经过点 A,则 FH= ( )

A.1.2 里
B.1.5 里
C.1.05 里
D.1.02 里

答案： C

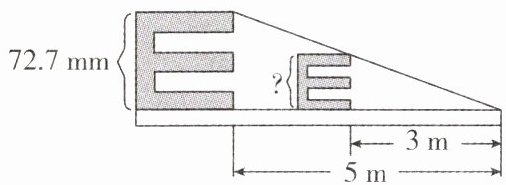
9. 如图,小明探究“制作视力表”的相关内容：当测试距离为 5 m 时,标准视力表中对应的最大的“E”字高度为 72.7 mm,当测试距离为 3 m 时,对应的最大的“E”字高度为______.

答案： 43.62mm

10. 幼儿园购买了一个板长 AB 为 4 m、支架 OC 高 0.8 m 的跷跷板(如图所示),支点 O 在板 AB 的中点处. 因为支架过高不宜小朋友玩,故把它暂时存放在高 2.4 m 的车库里准备改装. 现有几个小朋友把板的一端 A 按到地面上.
(1)板的另一端 B 会不会碰到车库的顶部？
(2)能否通过移动支架,使点 B 恰好碰到车库的顶部？若能,求出此时支点 O 的位置；若不能,请说明理由.

答案： 解：
(1)如图所示，过点B作BD⊥AC交AC的延长线于点D.
∵OC⊥AC，
∴OC//BD，
∴△AOC∽△ABD，
∴$\frac{OC}{BD}=\frac{AO}{AB}$.
∵AO=OB=2m，OC=0.8m，
∴BD=1.6m＜2.4m，
∴板的另一端B不会碰到车库顶部.
(2)能.理由如下：
∵BD=2.4m，
∴$\frac{AO}{AB}=\frac{OC}{BD}$，即$\frac{AO}{4}=\frac{0.8}{2.4}$，
∴AO=$\frac{4}{3}$m，即此时支点O到点A的距离是$\frac{4}{3}$m.