《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 用计算器求下列各式的值(精确到0.000 1)：
(1)$ \cos 38^{\circ}39' $.
(2)$ \sin 69^{\circ}12'51''+\cos 31^{\circ}21'10'' $.
(3)$ \tan 25^{\circ}+\tan 25'+\tan 25'' $.

答案：
(1)
首先保证计算器角度单位为度；
将$38^{\circ}39'$转化为度，$38^{\circ}39' = 38+\frac{39}{60}=38.65^{\circ}$；
用计算器求$\cos38.65^{\circ}\approx0.7801$。
(2)
角度单位设为度；
$69^{\circ}12'51'' = 69+\frac{12}{60}+\frac{51}{3600}=69.214167^{\circ}$；
$31^{\circ}21'10'' = 31+\frac{21}{60}+\frac{10}{3600}=31.352778^{\circ}$；
$\sin69.214167^{\circ}\approx0.9350$，$\cos31.352778^{\circ}\approx0.8544$；
$\sin69^{\circ}12'51''+\cos31^{\circ}21'10''\approx0.9350 + 0.8544=1.7894$。
(3)
角度单位设为度；
$25'=\frac{25}{60}\approx0.4167^{\circ}$，$25''=\frac{25}{3600}\approx0.0069^{\circ}$；
$\tan25^{\circ}\approx0.4663$，$\tan25'\approx\tan0.4167^{\circ}\approx0.0073$，$\tan25''\approx\tan0.0069^{\circ}\approx0.0001$；
$\tan25^{\circ}+\tan25'+\tan25''\approx0.4663+0.0073 + 0.0001=0.4737$。

10. 用计算器求 $ \sin 15^{\circ} $,$ \sin 25^{\circ} $,$ \sin 35^{\circ} $,$ \sin 45^{\circ} $,$ \sin 55^{\circ} $,$ \sin 65^{\circ} $,$ \sin 75^{\circ} $,$ \sin 85^{\circ} $的值,研究 $ \sin \alpha $ 的值随锐角 $ \alpha $ 变化的规律,根据这个规律判断：若$ \frac{1}{2}＜\sin \alpha＜\frac{\sqrt{3}}{2} $,则( )

A.$ 30^{\circ}＜\alpha＜60^{\circ} $
B.$ 30^{\circ}＜\alpha＜90^{\circ} $
C.$ 0^{\circ}＜\alpha＜60^{\circ} $
D.$ 60^{\circ}＜\alpha＜90^{\circ} $

答案： A

11. 如图,某厂房屋顶人字架的跨度 $ BC= 16 \ m $,上弦 $ AB= AC $,$ \angle BAC= 130^{\circ} $.小明想用科学计算器求上弦 $ AB $ 的长,若小明按键的顺序为8÷□65= ,则由左到右第三个方框中应按键的符号是______.(请从 $ \tan $,$ \sin $,$ \cos $ 中选择一个填写)

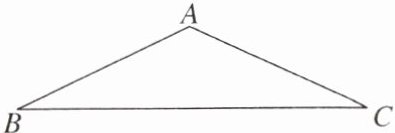
答案： sin

12. 为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯 $ AB $ 可伸缩(最长可伸至20 m),且可绕点 $ B $ 转动,其底部 $ B $ 离地面的距离 $ BC $ 为2 m,当云梯顶端 $ A $ 在建筑物 $ EF $ 所在直线上时,底部 $ B $ 到 $ EF $ 的距离 $ BD $ 为9 m.


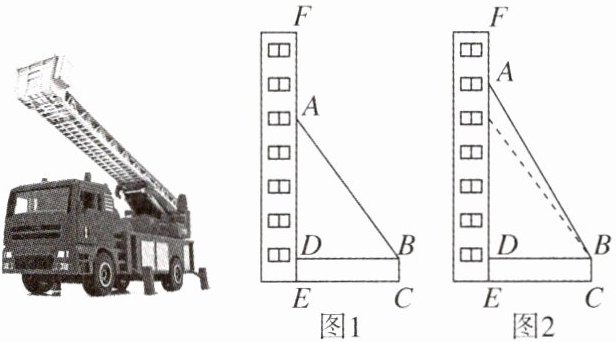
(1)若$ \angle ABD= 53^{\circ} $,求此时云梯 $ AB $ 的长.
(2)如图2,若在建筑物底部 $ E $ 的正上方19 m 处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处？请说明理由.(参考数据：$ \sin 53^{\circ}\approx0.8 $,$ \cos 53^{\circ}\approx0.6 $,$ \tan 53^{\circ}\approx1.3 $)

答案：
(1)15m；
(2)能。