《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. (1)已知 $a= 4$,$c= 9$,若 $b$ 是 $a,c$ 的比例中项,求 $b$ 的值.
(2)已知线段 $MN$ 是 $AB,CD$ 的比例中项,$AB= 4\ cm$,$CD= 5\ cm$,求 $MN$ 的长,并思考(1)(2)两题有何区别.

答案： 解:
(1)$\because b$是$a,c$的比例中项,
$\therefore a:b=b:c$,$\therefore b^{2}=ac$,
$\therefore b=\pm\sqrt{ac}$.
$\because a=4$,$c=9$,$\therefore b=\pm\sqrt{36}=\pm6$,即$b=\pm6$.
(2)$\because MN$是线段,$\therefore MN＞0$.
$\because$线段$MN$是$AB,CD$的比例中项,
$\therefore MN^{2}=AB\cdot CD$,$\therefore MN=\sqrt{AB\cdot CD}$.
$\because AB=4\ cm$,$CD=5\ cm$,
$\therefore MN=\sqrt{20}=2\sqrt{5}\ cm$.
通过解答
(1),
(2)发现,$b,MN$同时作为比例中项出现,$b$可以取负值,而线段$MN$的长不可以取负值.

10. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,$P$ 为 $AB$ 的黄金分割点($AP ＞ PB$),则下列结论中正确的是( )


A.$AB^2= AP^2 + BP^2$
B.$BP^2= AP\cdot BA$
C.$\frac{AP}{BP}= \frac{\sqrt{5}-1}{2}$
D.$\frac{BP}{AP}= \frac{\sqrt{5}-1}{2}$

答案： D

11. 如图,在 $Rt\triangle ABC$ 中,$\angle ABC= 90°$,$AB= 1$,$BC= \frac{1}{2}$.
进行如下操作：
①以点 $C$ 为圆心,以 $BC$ 的长为半径画弧,交 $AC$ 于点 $D$；
②以点 $A$ 为圆心,以 $AD$ 的长为半径画弧,交 $AB$ 于点 $E$.
则点 $E$ 是线段 $AB$ 的黄金分割点.
根据以上操作,$AE$ 的长为______.

答案： $\frac{\sqrt{5}-1}{2}$

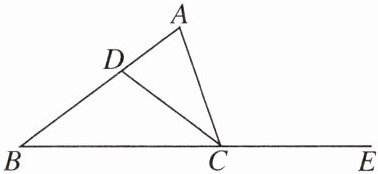
12. 如图,在 $\triangle ABC$ 中,点 $D$ 在边 $AB$ 上,且 $BD= DC= AC$,已知 $\angle ACE= 108°$,$BC= 2$.
(1)求 $\angle B$ 的度数.
(2)我们把有一个内角等于 $36°$ 的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比 $\frac{\sqrt{5}-1}{2}$.
①写出图中所有的黄金三角形,选一个说明理由.
②求 $AD$ 的长.

答案： 解:
(1)设$\angle B=x$,$\because BD=DC$,
$\therefore \angle DCB=\angle B=x$,
$\therefore \angle ADC=\angle B+\angle DCB=2x$.
$\because AC=DC$,$\therefore \angle A=\angle ADC=2x$.
$\because \angle ACE=\angle B+\angle A$,
$\therefore x+2x=108^{\circ}$,解得$x=36^{\circ}$,
即$\angle B=36^{\circ}$.
(2)①$\triangle ABC$,$\triangle DBC$,$\triangle CAD$都是黄金三角形.
理由如下:
$\because DB=DC$,$\angle B=36^{\circ}$,$\therefore \triangle DBC$为黄金三角形.
$\because \angle BCA=180^{\circ}-\angle ACE=72^{\circ}$,
而$\angle A=2×36^{\circ}=72^{\circ}$,
$\therefore \angle A=\angle ACB$,而$\angle B=36^{\circ}$,
$\therefore \triangle ABC$为黄金三角形.
$\because \angle ACD=\angle ACB-\angle DCB=72^{\circ}-36^{\circ}=36^{\circ}$,而$CA=CD$,
$\therefore \triangle CAD$为黄金三角形.
②$\because \triangle BAC$为黄金三角形,
$\therefore \frac{AC}{BC}=\frac{\sqrt{5}-1}{2}$.
又$\because BC=2$,$\therefore AC=\sqrt{5}-1$,
$\therefore BD=CD=CA=\sqrt{5}-1$,
$\therefore AD=AB-BD=2-(\sqrt{5}-1)=3-\sqrt{5}$.