《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

10. 如图,A,O 在网格中小正方形的顶点处,每个小方格的边长为 1,在此网格中找两个格点(即小正方形的顶点)B,C,使 O 为 $\triangle ABC$ 的外心,则 BC 的长度是( )

A.$3\sqrt{2}$
B.$2\sqrt{5}$
C.4
D.$\sqrt{17}$

答案：
A【解析】
∵点O为$\triangle ABC$的外心,
$\therefore OA=OB=OC$,点B和点C的位置如图所示:

$\therefore BC=\sqrt {3^{2}+3^{2}}=3\sqrt {2}.$

11. 如图,方格纸上每个小正方形的边长均为 1 个单位长度,点 O,A,B,C 在格点(两条网格线的交点叫格点)上,以点 O 为原点建立直角坐标系,则过 A,B,C 三点的圆的圆心坐标为______.

答案： (-1,-2)

12. 小明家的房前有一块矩形的空地,空地上有三棵树 A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).

答案：
解:如图所示.①分别以A,B为圆心,大于$\frac {1}{2}AB$的长为半径画弧,两弧相交于D,E两点,作直线DE;
②分别以A,C为圆心,大于$\frac {1}{2}AC$的长为半径画弧,两弧相交于G,F两点,作直线GF;
③直线DE与GF相交于点O,以O为圆心,OA的长为半径画圆,则此圆即为花坛的位置.

13. 在等腰三角形 $ABC$ 中,$AB= AC= 13\ cm$,$BC= 10\ cm$,求等腰三角形 $ABC$ 外接圆的半径.

答案：
解:如图,设O为$\triangle ABC$的外心,连结AO并延长交BC于点D,连结OB,OC,
∵AB=AC,O为$\triangle ABC$的外心,

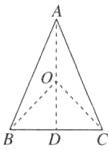
$\therefore AD⊥BC,BD=DC=\frac {1}{2}BC=5,$
设等腰三角形ABC外接圆的半径为R,
则OA=OB=OC=R,
在$Rt\triangle ABD$中,由勾股定理得$AD=\sqrt {AB^{2}-BD^{2}}=\sqrt {13^{2}-5^{2}}=12.$
在$Rt\triangle OBD$中,由勾股定理得$OB^{2}=OD^{2}+BD^{2},$
即$R^{2}=(12-R)^{2}+5^{2},R=\frac {169}{24},$
即等腰三角形ABC外接圆的半径为$\frac {169}{24}.$