《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

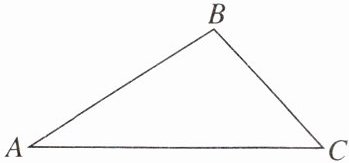
8. 如图,有一个三角形钢架ABC,∠A= 30°,∠C= 45°,AC= 2($\sqrt{3}$+1)m. 请计算说明工人师傅搬运此钢架能否通过一个直径为2.1 m的圆形门.

答案：
解:工人师傅搬运此钢架能通过一个直径为2.1m的圆形门.
理由:如图,过点B作BD⊥AC于点D.
∵AB＞BD,BC＞BD,AC＞AB＞BC,
∴求出DB的长,然后和2.1m比较即可.
设BD=xm,
∵∠A=30°,∠C=45°,
∴DC=BD=xm,AD=$\sqrt{3}$BD=$\sqrt{3}$xm.
∵AC=2($\sqrt{3}$+1)m,
∴x+$\sqrt{3}$x=2($\sqrt{3}$+1),
∴x=2,即BD=2m＜2.1m,
∴工人师傅搬运此钢架能通过一个直径为2.1m的圆形门.

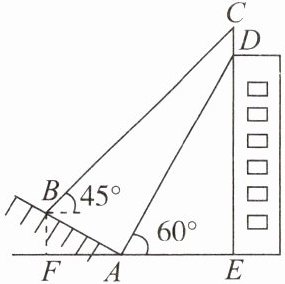
9. 如图,某建筑物的顶部有一块宣传牌CD,小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,AB= 10米,AE= 15米,则宣传牌CD的高度是( )


A.(20-10$\sqrt{3}$)米
B.(20+5$\sqrt{3}$)米
C.(15+5$\sqrt{3}$)米
D.(15$\sqrt{3}$-5)米

答案： A

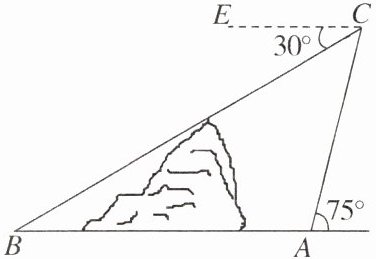
10. 如图,在小山的东侧点A处有一个热气球,由于受西风的影响,以30 m/min的速度沿与地面成75°角的方向飞行,20 min后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为______.

答案：
600$\sqrt{2}$m　[解析]如图,过点A作AD⊥BC,垂足为D.
在Rt△ACD中,∠ACD=75°−30°=45°,
AC=30×20=600(m),
∴AD=AC·sin45°=300$\sqrt{2}$m.
在Rt△ABD中,
∵∠B=30°,
∴AB=2AD=600$\sqrt{2}$m.

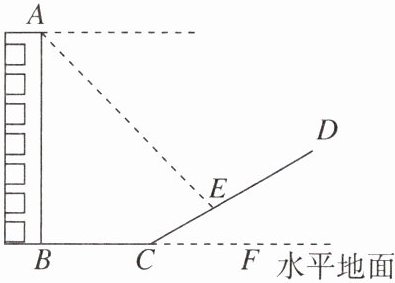
11. 如图,建筑物AB后有一座小山,∠DCF= 30°,测得小山坡脚C点与建筑物的水平距离BC= 25米,若山坡上E点处有一凉亭,且凉亭与坡脚距离CE= 20米,某人从建筑物顶端A点测得E点处的俯角为48°.
(1)求凉亭到地面的距离.
(2)求建筑物AB的高.(结果精确到0.1米)
(参考数据：$\sqrt{3}\approx1.73$,sin 48°≈0.74,cos 48°≈0.67,tan 48°≈1.11,sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)

答案：

(1)过点E作EM⊥BF于M,如图.
∵∠DCF=30°,CE=20米,
∴EM=CE·sin30°=10米.
答:凉亭到地面的距离为10米.

(2)过E作EN⊥AB,交AB于点N,则BN=EM =10米,NE=BM,∠BNE=90°.
在Rt△CME中,CM=CE·cos30°=10$\sqrt{3}$米,
∴NE=BM=BC+CM=(25+10$\sqrt{3}$)米.
记α为在A点测得E点处的俯角,则α=48°,
∴∠EAN=90°−α=42°.
在Rt△ANE中,
AN=$\frac{NE}{\tan42°}$≈$\frac{25+10\sqrt{3}}{0.9}$≈47.0(米),
∴AB=AN+BN≈57.0米.
答:建筑物AB的高约为57.0米.