《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

8. 如图,G是△ABC的重心,过点G作$EF // BC$,分别交AB,AC于点E,F,且$EF + BC = 7.2\ cm$,求BC的长.
]

答案： 解:如图，连结AG并延长，交BC于点P.
∵G是△ABC的重心,
∴AG=2GP,
∴$\frac{AG}{AP}=\frac{2}{3}$.
∵EF过点G且EF//BC,
∴△AGF∽△APC,△AEF∽△ABC,
∴$\frac{AF}{AC}=\frac{AG}{AP}=\frac{2}{3}$,
∴$\frac{EF}{BC}=\frac{AF}{AC}=\frac{2}{3}$.又
∵EF+BC=7.2cm,
∴$BC=\frac{3}{5}×7.2=4.32$(cm).

9. 三边的长分别为3,4,5的△ABC,它的重心为$O_1$,外心为$O_2$,则$O_1O_2$的长是 ( )

A.$\frac{5}{2}$
B.$\frac{5}{4}$
C.$\frac{5}{6}$
D.$\frac{5}{3}$

答案： C

10. 如图,点G是△ABC的重心,$GE // AB$交BC于点E,$GF // AC$交BC于点F,若△GEF的周长是2,则△ABC的周长为______.
]

答案： 6

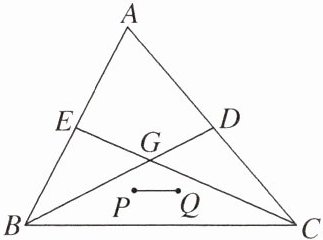
11. 如图,G是△ABC的重心,延长BG交AC于点D,延长CG交AB于点E,P,Q分别是△BCE和△BCD的重心,则$\frac{PQ}{BC}= $______.
]

答案： $\frac{1}{6}$

12. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,$AG \perp BC$于点G,$AF \perp DE$于点F,$\angle EAF = \angle GAC$.
(1)求证：$\triangle ADE \backsim \triangle ABC$.
(2)若$AD= 3,AB= 5$,求$\frac{AF}{AG}$的值.
]

答案：
(1)证明:
∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,
∴∠AED=∠ACB.
∵∠EAD=∠CAB,
∴△ADE∽△ABC.
(2)由
(1)可知,△ADE∽△ABC,
∴$\frac{AE}{AC}=\frac{AD}{AB}=\frac{3}{5}$.又
∵∠AFE=∠AGC=90°,∠EAF=∠GAC,
∴△EAF∽△CAG,
∴$\frac{AF}{AG}=\frac{AE}{AC}$,
∴$\frac{AF}{AG}=\frac{3}{5}$.