第33页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
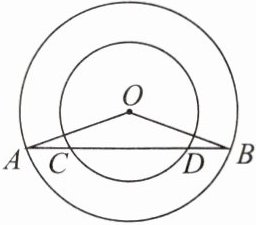
9. 如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC= BD.
(2)若AC= 3,大圆和小圆的半径分别为6和4,求CD的长度.
(1)求证:AC= BD.
(2)若AC= 3,大圆和小圆的半径分别为6和4,求CD的长度.

答案:
解:
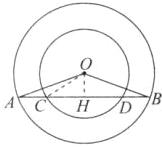
(1)证明:过点O作OH⊥CD于点H,如图,
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH - CH=BH - DH,
∴AC=BD.
(2)连结OC,如图,设CH=x,
在Rt△OCH中,$OH^{2}=OC^{2}-CH^{2}=4^{2}-x^{2}$,
在Rt△OAH中,$OH^{2}=OA^{2}-AH^{2}=6^{2}-(3 + x)^{2}$,
∴$4^{2}-x^{2}=6^{2}-(3 + x)^{2}$,解得$x=\frac{11}{6}$,
∴$CD = 2CH=\frac{11}{3}$.
解:
(1)证明:过点O作OH⊥CD于点H,如图,
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH - CH=BH - DH,

∴AC=BD.
(2)连结OC,如图,设CH=x,
在Rt△OCH中,$OH^{2}=OC^{2}-CH^{2}=4^{2}-x^{2}$,
在Rt△OAH中,$OH^{2}=OA^{2}-AH^{2}=6^{2}-(3 + x)^{2}$,
∴$4^{2}-x^{2}=6^{2}-(3 + x)^{2}$,解得$x=\frac{11}{6}$,
∴$CD = 2CH=\frac{11}{3}$.
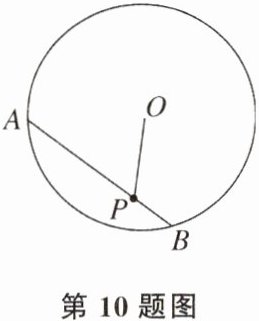
10. 如图,已知⊙O的半径为10,⊙O的一条弦AB= 16,若⊙O内的一点P恰好在AB(点P不与A,B重合)上,则线段OP的长度为整数的值有( )
A.2个
B.3个
C.4个
D.5个

A.2个
B.3个
C.4个
D.5个
答案:
C
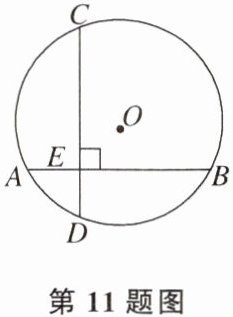
11. 如图,⊙O的弦AB垂直于CD,E为垂足,AE= 3,BE= 7,且AB= CD,则圆心O到CD的距离是______.

答案:
2
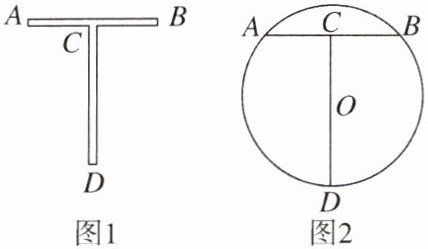
12. 丁字尺是一种作图工具,图1所示为丁字尺,可以看作由两把互相垂直的直尺组成,并且CD部分平分AB部分.现在将丁字尺放在一个圆形工件上(圆心为O),如图2,使得点A,B,D分别落在⊙O上,这样圆心O就会落在CD上,已知AB= CD= 8cm,请求出该圆形工件的半径.

答案:
解:
∵圆心O落在CD上,CD平分AB,
∴线段CD垂直平分线段AB,
∵A,B,D三点所在圆的圆心O在CD上,
∴AC=BC=$\frac{1}{2}AB=\frac{1}{2}×8 = 4$(cm),
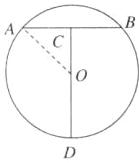
如图,连结AO,则$AC^{2}+OC^{2}=AO^{2}$.
设⊙O的半径为r(cm),
∵CD = 8cm,
∴OC=(8 - r)cm,
∴$4^{2}+(8 - r)^{2}=r^{2}$,
解得r = 5,
∴该圆形工件的半径为5cm.
解:
∵圆心O落在CD上,CD平分AB,
∴线段CD垂直平分线段AB,
∵A,B,D三点所在圆的圆心O在CD上,
∴AC=BC=$\frac{1}{2}AB=\frac{1}{2}×8 = 4$(cm),
如图,连结AO,则$AC^{2}+OC^{2}=AO^{2}$.
设⊙O的半径为r(cm),
∵CD = 8cm,

∴OC=(8 - r)cm,
∴$4^{2}+(8 - r)^{2}=r^{2}$,
解得r = 5,
∴该圆形工件的半径为5cm.
13. 如图,∠PAC= 30°,在射线AC上顺次截取AD= 3cm,DB= 10cm,以DB为直径作⊙O交射线AP于E,F两点.
(1)求圆心O到AP的距离.
(2)求弦EF的长.
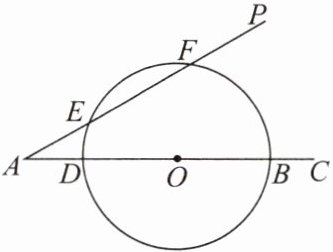
(1)求圆心O到AP的距离.
(2)求弦EF的长.

答案:
解:
(1)过点O作OH⊥EF于点H,如图,
∵DB = 10cm,
∴OD = 5cm,
∴OA = AD + OD = 3 + 5 = 8(cm).
在Rt△OAH中,
∵∠OAH = 30°,
∴$OH=\frac{1}{2}OA = 4$cm,
即圆心O到AP的距离为4cm.
(2)连结OF,如图,
∵OH⊥EF,
∴EH = FH.
在Rt△OHF中,$HF=\sqrt{OF^{2}-OH^{2}}=\sqrt{5^{2}-4^{2}} = 3$(cm),
∴EF = 2HF = 6cm.
(1)过点O作OH⊥EF于点H,如图,
∵DB = 10cm,
∴OD = 5cm,
∴OA = AD + OD = 3 + 5 = 8(cm).
在Rt△OAH中,
∵∠OAH = 30°,
∴$OH=\frac{1}{2}OA = 4$cm,
即圆心O到AP的距离为4cm.
(2)连结OF,如图,
∵OH⊥EF,
∴EH = FH.
在Rt△OHF中,$HF=\sqrt{OF^{2}-OH^{2}}=\sqrt{5^{2}-4^{2}} = 3$(cm),
∴EF = 2HF = 6cm.
查看更多完整答案,请扫码查看


