《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

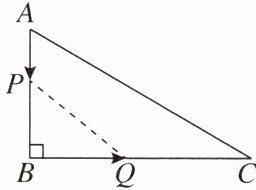
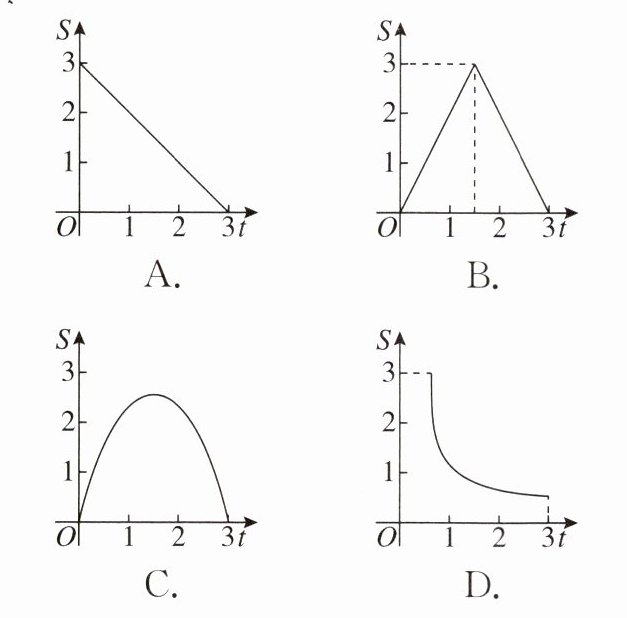
9. 如图,在$\triangle ABC$中,$\angle B= 90^{\circ}$,$AB= 3\ cm$,$BC= 6\ cm$,动点$P从点A$出发,沿$AB向点B$以1 cm/s的速度移动,动点$Q从点B$出发,沿$BC向点C$以2 cm/s的速度移动。若$P$,$Q两点分别从A$,$B$两点同时出发,当点$P到达点B$时两点同时停止运动,则$\triangle PBQ的面积S与出发时间t$的函数关系图象大致是 ( )




A.
B.
C.
D.

答案： C【解析】由题意可知，PB=(3-t)cm，BQ=2t(cm)，
∴S△PBQ=1/2PB·BQ=1/2(3-t)·2t=-t²+3t(0≤t≤3)，故选C.

10. 如图,线段$AB= 8\ cm$,$C是AB$上一点,$D$,$E分别是AC$的三等分点,分别以$AD$,$DE$,$EC$,$CB$为边作正方形,设$AD为x\ cm$,四个正方形的面积之和为$S$。

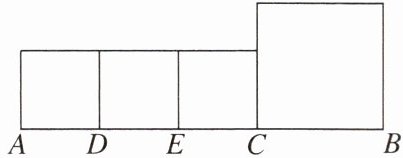
(1)$S关于x$的函数表达式为______,自变量$x$的取值范围是______。
(2)当$AD= $______$cm$时,四个正方形的面积之和最小,最小值是______$cm^{2}$。

答案：
(1)S=12x²-48x+64 0＜x＜8/3
(2)2 16

11. 有一个窗户形状如图1,上部是由两个正方形组成的矩形,下部是一个矩形。如果制作窗框的材料总长为6 m,利用图2,解答下列问题：


(1)若$AB$为1 m,求此时窗户的透光面积。
(2)如何设计这个窗户,使透光面积最大？请通过计算说明。

答案： 解：
(1)由已知可得AD=(6-1-1-1-1/2)/2=5/4(m)，则S=1×5/4=5/4(m²)，故此时窗户的透光面积为5/4m².
(2)设AB=x m，则AD=(3-7/4x)m，
∵3-7/4x＞0，
∴0＜x＜12/7.设窗户面积为S m²，由已知得S=AB·AD=x(3-7/4x)=-7/4x²+3x=-7/4(x-6/7)²+9/7，当x=6/7m时，S最大值=9/7m².
∴3-7/4x=3/2.
∴AB=6/7m，AD=3/2m，上部两个正方形的边长为3/7m时，透光面积取最大值，最大值为9/7m².