第52页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 如图,下列条件中,不能判定$\triangle ACD\backsim\triangle ABC$的是( )
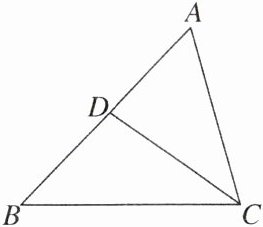
A.$\angle ACD= \angle B$
B.$\frac{AD}{AC}= \frac{CD}{BC}$
C.$\angle ADC= \angle ACB$
D.$\frac{AC}{AD}= \frac{AB}{AC}$

A.$\angle ACD= \angle B$
B.$\frac{AD}{AC}= \frac{CD}{BC}$
C.$\angle ADC= \angle ACB$
D.$\frac{AC}{AD}= \frac{AB}{AC}$
答案:
B
2. 如图,下列能判定$BC// ED$的条件是( )
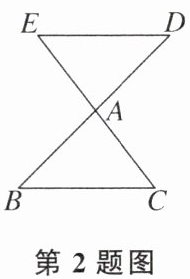
A.$\frac{EC}{BD}= \frac{AD}{AB}$
B.$\frac{EC}{BD}= \frac{AE}{AC}$
C.$\frac{AD}{BD}= \frac{AE}{AC}$
D.$\frac{AD}{AB}= \frac{AE}{AC}$

A.$\frac{EC}{BD}= \frac{AD}{AB}$
B.$\frac{EC}{BD}= \frac{AE}{AC}$
C.$\frac{AD}{BD}= \frac{AE}{AC}$
D.$\frac{AD}{AB}= \frac{AE}{AC}$
答案:
D
3. 如图,下列四个三角形中相似的三角形是( )
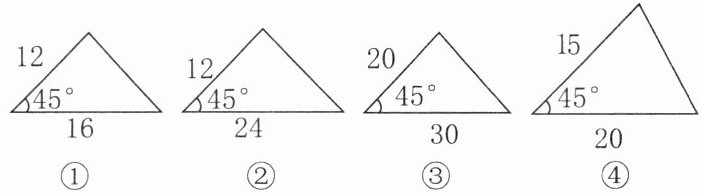
A.①和②
B.①和④
C.③和④
D.①和④,②和③

A.①和②
B.①和④
C.③和④
D.①和④,②和③
答案:
B
4. 如图,已知$\angle 1= \angle 2$,添加下列条件后,仍无法判定$\triangle ABC\backsim\triangle ADE$的是( )
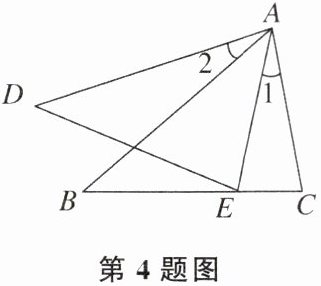
A.$\frac{AB}{AC}= \frac{AD}{AE}$
B.$\angle B= \angle D$
C.$\angle C= \angle AED$
D.$\frac{AB}{AD}= \frac{BC}{DE}$

A.$\frac{AB}{AC}= \frac{AD}{AE}$
B.$\angle B= \angle D$
C.$\angle C= \angle AED$
D.$\frac{AB}{AD}= \frac{BC}{DE}$
答案:
D
5. 如图,四边形$ABCD的对角线AC$,$BD相交于点O$,且将这个四边形分成①,②,③,④四个三角形.若$OA:OC= OB:OD$,则下列结论中,一定成立的是( )

A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似

A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
答案:
B
6. 如图,在$\triangle ABC$中,点$D为边AC$上的一点,选择下列条件:①$\angle 2= \angle A$.②$\angle 1= \angle CBA$.③$\frac{BC}{AC}= \frac{CD}{AB}$.④$\frac{BC}{AC}= \frac{CD}{BC}$中的一个,其中,不能得出$\triangle ABC和\triangle BCD$相似的是 ______ .(填序号)
]
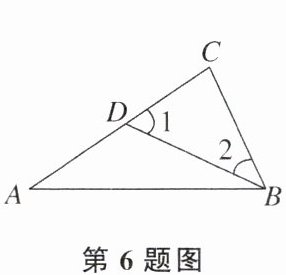
]

答案:
③
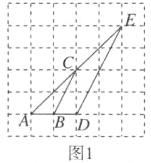
7. 如图,已知$\frac{AB}{AC}= \frac{AC}{AD}= k$,请再添加一个条件,使$\triangle ABC\backsim\triangle ACD$,你添加的条件是 ______ .(写出一个即可)
]

]

答案:
∠BAC=∠CAD(或 AC 平分∠BAD)
8. 如图,在$6× 6$的正方形网格中,点$A,B,C$均在格点上,请按要求作图.
(1)在图1中画一个格点$\triangle ADE$,使$\triangle ADE\backsim\triangle ABC$.
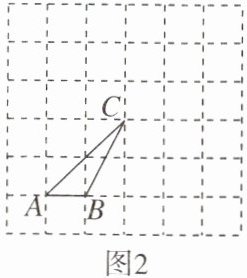
(2)在图2中画一条格点线段$BP$,交$AC于点Q$,使$CQ= 2AQ$.
]
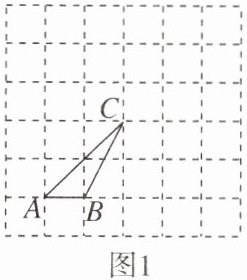
(1)在图1中画一个格点$\triangle ADE$,使$\triangle ADE\backsim\triangle ABC$.
(2)在图2中画一条格点线段$BP$,交$AC于点Q$,使$CQ= 2AQ$.
]


答案:
解:
(1)如图1所示,△ADE 即为所求.
(2)如图2所示,线段 BP 即为所求.
解:
(1)如图1所示,△ADE 即为所求.

(2)如图2所示,线段 BP 即为所求.
查看更多完整答案,请扫码查看


