《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 如图,在$\triangle ABC$中,$AB= 4$,$BC= 8$,$D为BC$边上一点,$BD= 2$.求证:$\angle BDA= \angle BAC$.
]

答案： 证明:在△ABC 中,AB=4,BC=8,BD=2,
∴ $\frac{AB}{BC}=\frac{4}{8}=\frac{1}{2}$,$\frac{BD}{BA}=\frac{2}{4}=\frac{1}{2}$,
∴ $\frac{AB}{BC}=\frac{BD}{BA}$.
又
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴∠BDA=∠BAC.

10. 如图,$AB是\odot O$的直径,$D,E$是半圆上任意两点,连结$AD,DE,AE与BD相交于点C$,要使$\triangle ADC与\triangle ABD$相似,可以添加一个条件.下列添加的条件中错误的是( )


A.$\angle ACD= \angle DAB$
B.$AD= DE$
C.$AD\cdot AB= CD\cdot BD$
D.$AD^{2}= BD\cdot CD$

答案： C

11. 如图,在四边形$ABCD$中,$AD// BC$.爱思考的小聪学了本节课后,进行了如下推理:
$\because AD// BC$,$\therefore\triangle AOD\backsim\triangle COB$,$\therefore\frac{AO}{CO}= \frac{DO}{BO}$.又$\because\angle AOB= \angle DOC$,$\therefore\triangle AOB\backsim\triangle DOC$.
你认为小聪的推理正确吗？写出你的观点.
]

答案： 解:不正确.理由如下:
$\frac{AO}{CO}=\frac{DO}{BO}$与∠AOB=∠DOC 不能构成△AOB∽△DOC 的条件,因为边的对应关系错误.

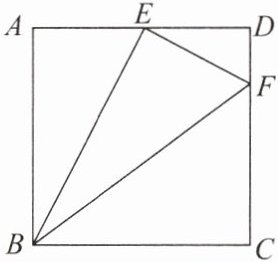
12. 如图,在正方形$ABCD$中,$E是AD$的中点,点$F在CD$上,且$CF= 3FD$.
(1)求证:$\triangle ABE\backsim\triangle DEF$.
(2)$\triangle ABE与\triangle BEF$相似吗？为什么？
]

答案： 解:
(1)证明:
∵四边形 ABCD 为正方形,
∴∠A=∠D=90°,AB=AD=CD.
设 AB=AD=CD=4a,
∵E 为边 AD 的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴$\frac{AB}{DE}=\frac{4a}{2a}=2$,$\frac{AE}{DF}=\frac{2a}{a}=2$,
∴$\frac{AB}{DE}=\frac{AE}{DF}$.
又
∵∠A=∠D=90°,
∴△ABE∽△DEF.
(2)相似.理由如下:
∵△ABE∽△DEF,
∴$\frac{EF}{BE}=\frac{DE}{AB}=\frac{1}{2}$,∠ABE=∠DEF.
∵∠AEB=∠DFE,∠ABE=∠DEF,
∠AEB+∠DEF=∠AEB+∠ABE=90°,
∴∠BEF=90°.
又
∵$\frac{AE}{AB}=\frac{EF}{BE}=\frac{1}{2}$,∠A=∠BEF=90°,
∴△ABE∽△EBF.