第10页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 在一个边长为2的正方形中挖去一个边长为$x(0<x<2)$的小正方形,如果设剩余部分的面积为$y$,那么$y关于x$的函数表达式是 ( )
A.$y= x^{2}$
B.$y= 4-x^{2}$
C.$y= x^{2}-4$
D.$y= 4-2x$
A.$y= x^{2}$
B.$y= 4-x^{2}$
C.$y= x^{2}-4$
D.$y= 4-2x$
答案:
B
2. 如图,某中学教学楼前喷水池喷出的水柱为抛物线形,其函数表达式为$y= -(x-2)^{2}+6$,则水柱的最大高度是 ( )
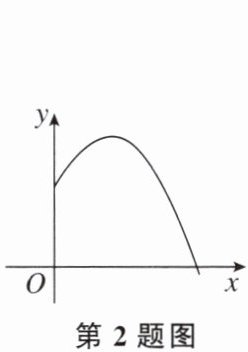
A.2
B.4
C.6
D.$2+\sqrt{6}$

A.2
B.4
C.6
D.$2+\sqrt{6}$
答案:
C
3. 如图,这是一个二次函数的图象$(0\leq x\leq3)$,关于该函数在所给自变量取值范围内,下列说法正确的是( )
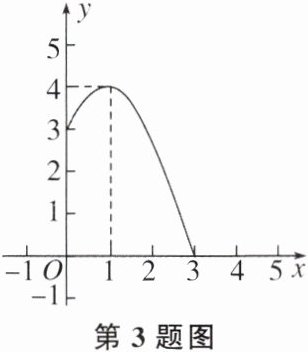
A.有最小值0,有最大值3
B.有最小值0,有最大值4
C.有最小值1,有最大值3
D.无最小值,有最大值4

A.有最小值0,有最大值3
B.有最小值0,有最大值4
C.有最小值1,有最大值3
D.无最小值,有最大值4
答案:
B
4. 某烟花厂特别设计制作了一种新型礼炮,这种礼炮的升空高度$h(m)与飞行时间t(s)的关系式是h= -\frac{5}{2}t^{2}+20t+1$。若这种礼炮在点火升空到最高点处引爆,从点火升空到引爆需要的时间为 ( )
A.3 s
B.4 s
C.5 s
D.6 s
A.3 s
B.4 s
C.5 s
D.6 s
答案:
B
5. 如图,这是二次函数$y= -\frac{1}{2}x^{2}+\frac{3}{2}x+2$的图象,当$-1\leq x\leq0$时,该函数的最大值是 ( )
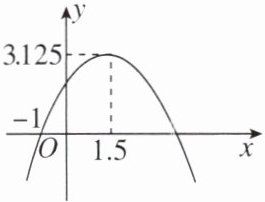
A.3.125
B.4
C.2
D.0

A.3.125
B.4
C.2
D.0
答案:
C
6. 科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
|温度$t/^{\circ}C$|-4|-2|0|1|4|
|植物高度增长量$l/mm$|41|49|49|46|25|
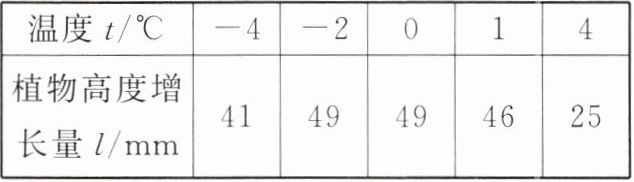
科学家推测出$l与t$之间是二次函数关系。由此可以推测出最适合这种植物生长的温度为______$^{\circ}C$。
|温度$t/^{\circ}C$|-4|-2|0|1|4|
|植物高度增长量$l/mm$|41|49|49|46|25|

科学家推测出$l与t$之间是二次函数关系。由此可以推测出最适合这种植物生长的温度为______$^{\circ}C$。
答案:
-1
7. 用一根长为20 cm的铁丝围成一个矩形,该矩形面积的最大值是______$cm^{2}$。
答案:
25
8. 已知二次函数$y= x^{2}$,当$-1\leq x\leq2$时,求函数$y$的最小值和最大值。
答案:
解:
∵y=x²,
∴该函数的图象开口向上,对称轴是y轴,
∵-1≤x≤2,
∴当x=0时取得最小值,最小值是0,当x=2时取得最大值,此时y=4.综上可得,当-1≤x≤2时,函数y的最小值是0,最大值是4.
∵y=x²,
∴该函数的图象开口向上,对称轴是y轴,
∵-1≤x≤2,
∴当x=0时取得最小值,最小值是0,当x=2时取得最大值,此时y=4.综上可得,当-1≤x≤2时,函数y的最小值是0,最大值是4.
查看更多完整答案,请扫码查看


