《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

1. 如图,在$\odot O$中,$OA= 2$,$\angle C= 45°$,则图中阴影部分的面积为( )


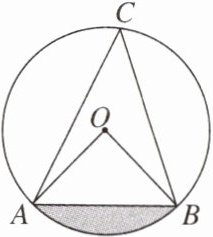
A.$\frac{\pi}{2}-\sqrt{2}$
B.$\pi-\sqrt{2}$
C.$\frac{\pi}{2}-2$
D.$\pi-2$

答案： D

2. 如图,AB是$\odot O$的直径,弦$CD\perp AB$,垂足为点M,连结OC,DB.如果$OC// DB$,$OC= 2\sqrt{3}$,那么图中阴影部分的面积是( )


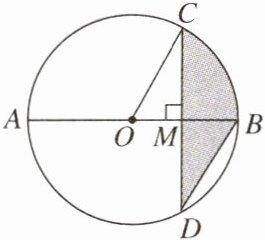
A.$\pi$
B.$2\pi$
C.$3\pi$
D.$4\pi$

答案： B

3. 如图,正方形的边长为a,以正方形边长为半径向外作四分之一圆,则阴影部分的面积可表示为______.(结果保留$\pi$)

答案： $\frac {1}{4}\pi a^{2}$

4. 如图,正方形ABCD的边长为6,它的中心为O,$\odot O$的半径为2.$OE\perp OF$于O,点E,F分别在AB,AD上,则图中阴影部分的面积为______.(结果保留$\pi$)

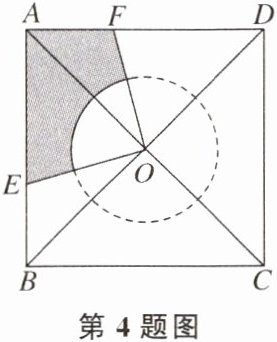
答案： $9-\pi$

5. 如图,从一张圆心角为$45°$的扇形纸板剪出一个边长为1的正方形CDEF,则图中阴影部分的面积为______.

答案：
$\frac {5}{8}\pi -\frac {3}{2}$【解析】连结 OF，$\because \angle AOD=45^{\circ }$,四边形 CDEF 是正方形，$\therefore CD=DE=EF,\angle OEF=\angle CDE=\angle CDO=90^{\circ },$$\therefore OD=CD=DE=EF.$在$Rt\triangle OFE$中,$OE=2EF=2,$$EF^{2}+OE^{2}=OF^{2},$$\therefore OF=\sqrt {OE^{2}+EF^{2}}=\sqrt {5},$$\therefore S_{阴影}=S_{扇形AOB}-S_{\triangle ODF}-S_{正方形CDEF}=\frac {45\pi \cdot (\sqrt {5})^{2}}{360}-\frac {1}{2}× 1× 1-1× 1=\frac {5}{8}\pi -\frac {3}{2}.$

6. 如图,圆心角都是$90°$的扇形AOB与扇形COD叠放在一起,连结AC,BD.
(1)求证:$AC= BD$.
(2)若图中阴影部分的面积是$\frac{3}{4}\pi\ cm^2$,$OA= 2\ cm$,求OC的长.

答案：
(1)证明:$\because \angle AOB=\angle COD=90^{\circ },$$\therefore \angle AOC+\angle AOD=\angle BOD+\angle AOD,$$\therefore \angle AOC=\angle BOD.$在$\triangle AOC$和$\triangle BOD$中,$\left\{\begin{array}{l} OA=OB\\ \angle AOC=\angle BOD\\ CO=DO\end{array}\right. $$\therefore \triangle AOC\cong \triangle BOD(SAS),\therefore AC=BD.$
(2)根据题意得,$S_{阴影}=S_{扇形AOB}+S_{\triangle AOC}-S_{扇形COD}-S_{\triangle BOD}=S_{扇形AOB}-S_{扇形COD}=\frac {90\pi \cdot OA^{2}}{360}-\frac {90\pi \cdot OC^{2}}{360}=\frac {90\pi \cdot (OA^{2}-OC^{2})}{360},$$\therefore \frac {3}{4}\pi =\frac {90\pi × (2^{2}-OC^{2})}{360}$,解得$OC=1$(负值舍去).