《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

1. 在△ABC中,D是边BC的中点,连结AD.若点O在AD上,且AO∶OD= 2∶1,则点O是△ABC的 ( )

A.垂心
B.外心
C.重心
D.中心

答案： C

2. 如图,下面的网格是由边长相同的小正方形组成的,点A,B,C,D,E,F,G均在小正方形的顶点上,则△ABC的重心是 ( )


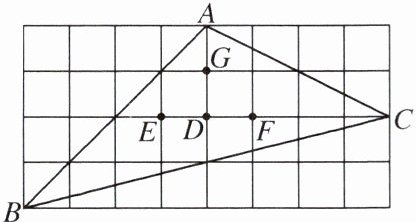
A.点G
B.点D
C.点E
D.点F

答案： B

3. 如图,已知D是△ABC的重心,则下列结论错误的是 ( )

A.$AD= 2DE$
B.$AE= 2DE$
C.$BE= CE$
D.$S_{\triangle ABE}= S_{\triangle ACE}$

答案： B

4. 如图,AD经过△ABC的重心,E是AC的中点,过点E作$EG // BC$交AD于点G,若$BC= 12$,则线段GE的长为 ( )


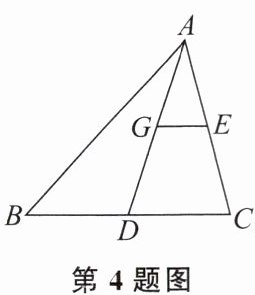
A.6
B.4
C.5
D.3

答案： D

5. 如图,在△ABC中,E在AD上,且E是△ABC的重心,若$S_{\triangle ABC}= 36$,则$S_{\triangle DEC}$等于 ( )


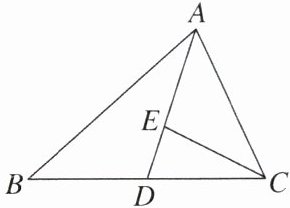
A.3
B.4
C.6
D.9

答案： C

6. 如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE相交于点G.若$DG= 2$,则AG= ______.
]

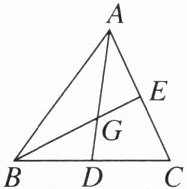
答案： 4

7. 求证：相似三角形对应边上的中线长之比等于相似比.
要求：画出图形,并据此写出已知、求证和证明过程.

答案： 解:如图.已知:△A'B'C'∽△ABC,$\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$,A'D'=D'B',AD=DB.求证:$\frac{D'C'}{DC}=k$.证明:
∵A'D'=D'B',AD=DB,
∴$A'D'=\frac{1}{2}A'B'$,$AD=\frac{1}{2}AB$,
∴$\frac{A'D'}{AD}=\frac{\frac{1}{2}A'B'}{\frac{1}{2}AB}=\frac{A'B'}{AB}=\frac{A'C'}{AC}$.在△A'D'C'和△ADC中,
∵$\frac{A'D'}{AD}=\frac{A'C'}{AC}$,且∠A'=∠A,
∴△A'D'C'∽△ADC,
∴$\frac{D'C'}{DC}=\frac{A'C'}{AC}=k$.