《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 有一段圆弧形的公路弯道,其所对的圆心角的度数为$120°$,半径为 2000 m,一辆汽车以 80 km/h 的速度开过这段弯道,需要多少分钟?(精确到 0.01)

答案： 解:$\frac{120×\pi×2000}{180}÷\frac{80×1000}{60}=\pi\approx3.14$(分钟). 答:需要3.14分钟.

10. 如图,$\odot O$的半径为 3,BC 是$\odot O$的弦,直径 AD⊥BC,$\angle D= 30°$,则$\widehat{BC}$的长为( )

A.$\frac{\pi}{2}$
B.$\pi$
C.$2\pi$
D.$3\pi$

答案： C

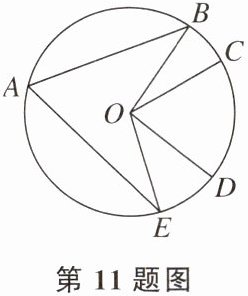
11. 如图,在半径为 1 的$\odot O$上顺次取点 A,B,C,D,E,连结 AB,AE,OB,OC,OD,OE. 若$\angle BAE= 65°$,$\angle COD= 70°$,则$\widehat{BC}与\widehat{DE}$的长度之和为______.

答案： $\frac{1}{3}\pi$

12. 如图,已知 AB 是$\odot O$的直径,弦 CD⊥AB 于点 E,如果$\angle A= 15°$,弦 CD= 4.
(1)求 AB 的长.
(2)求弧 CD 的长.

答案：
解:
(1)$\because CD\perp AB$, $\therefore CE=DE=\frac{1}{2}CD=2$,$\angle OEC=90°$. $\because \angle BOC=2\angle A=2×15°=30°$, $\therefore OC=2CE=4$,$\therefore AB=2OC=8$.
(2)如图,连结OD, $\because OC=OD$,$CD\perp AB$, $\therefore \angle COD=2\angle BOC=60°$, $\therefore \frac{60\pi×4}{180}=\frac{4}{3}\pi$. 答:弧CD的长为$\frac{4}{3}\pi$.