《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 一张圆桌旁设有 4 个座位,丙先坐在了④号座位上,如图,甲、乙 2 人等可能地坐到①,②,③中的 2 个座位上.
(1)甲坐在①号座位的概率是______.
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.

答案：
(1)$\frac{1}{3}$
(2)画树状图如下:乙 共有6种等可能的结果,甲与乙两人恰好相邻而坐的结果有4种,
∴甲与乙相邻而坐的概率为$\frac{4}{6}$=$\frac{2}{3}$.

10. 一个不透明的袋中装有 1 个红球、1 个黄球和 1 个黑球,它们除颜色外其余都相同.
(1)从袋中随机摸出两个球,求两个球的颜色恰好为一红一黑的概率.请利用树状图或列表法说明理由.
(2)如果从袋中随机摸出小球 3 次,每次摸出 1 个球,并且不放回,那么第 3 次为红球的概率为______.

答案：
(1)画树状图如下:第一个 第二个黄　　黑　红　　黑　红　　黄 共有6种等可能的结果,其中从袋中随机摸出两个球颜色恰好为一红一黑的有2种情况,
∴从袋中随机摸出两个球颜色恰好为一红一黑的概率是$\frac{2}{6}$=$\frac{1}{3}$.
(2)$\frac{1}{3}$

11.(1)一条线段如图 1 所示,AB 的长为 10 cm,MN 的长为 2 cm,假设可以随意在这条线段上取一点,求这个点取在线段 MN 上的概率.
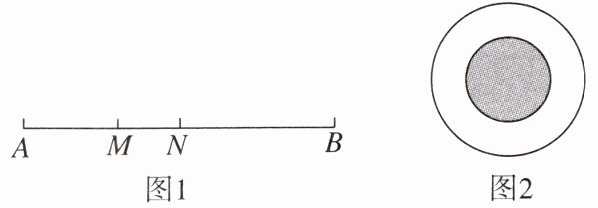
(2)图 2 是一个木制圆盘,图中有两个同心圆,其中大圆的直径为 20 cm,小圆的直径为 10 cm,一只在空中飞行的小鸟要落在这个木制圆盘上,求小鸟落在小圆内(阴影部分)的概率.

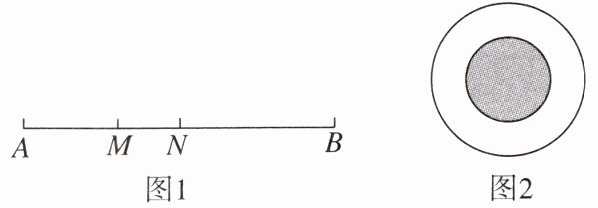
答案：
(1)AB的长为10cm,MN的长为2cm,故随意在这条线段上取一个点,那么这个点取在线段MN上的概率为$\frac{2}{10}$=$\frac{1}{5}$.
(2)
∵大圆的面积$S_{1}=π×(\frac{20}{2})^{2}=100π(cm^{2})$,小圆的面积$S_{2}=π×(\frac{10}{2})^{2}=25π(cm^{2})$,
∴小鸟落在小圆内的概率是$\frac{25π}{100π}=\frac{1}{4}$.