《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 一小球从地面抛出的运动路线呈抛物线形.当球离抛出地的水平距离为 10 m 时,达到最大高度 5 m,求球被抛出的距离.

答案： 解:根据题意,设抛物线的函数表达式为y=a(x-10)²+5,把(0,0)代入得a=-1/20,所以抛物线的函数表达式为y=-1/20(x-10)²+5.当y=0时,x₁=0,x₂=20.所以抛物线与x轴的交点为(0,0),(20,0).
∴球被抛出20 m.

10. 二次函数 $y= ax^2+bx(a≠0)$ 的图象如下图所示,若一元二次方程 $ax^2+bx-m= 0$ 有实数根,则 $m$ 的最小值为 ( )


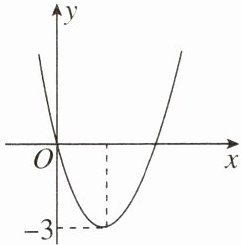
A.-3
B.3
C.-6
D.9

答案： A

11. 在利用图象法求方程 $x^2= \frac{1}{2}x+3$ 的解 $x_1,x_2$ 时,下面是四名同学的解法.
甲：函数 $y= x^2-\frac{1}{2}x-3$ 的图象与 $x$ 轴交点的横坐标是 $x_1,x_2$；
乙：函数 $y= x^2$ 与 $y= \frac{1}{2}x+3$ 的图象交点的横坐标是 $x_1,x_2$；
丙：函数 $y= x^2-3$ 与 $y= \frac{1}{2}x$ 的图象交点的横坐标是 $x_1,x_2$；
丁：函数 $y= x^2+1$ 与 $y= \frac{1}{2}x+4$ 的图象交点的横坐标是 $x_1,x_2$.
你认为解法正确的同学有 ______.

答案： 甲乙丙丁

12. 二次函数 $y= ax^2+bx+c(a≠0)$ 的部分对应值如下表所示：
| x | ... | -3 | 0 | 1 | 3 | 5 | ... |
| y | ... | 7 | -8 | -9 | -5 | 7 | ... |
则一元二次方程 $a(2x+1)^2+b(2x+1)+c= -5$ 的解为 ______.

答案： x=±1

13. 二次函数 $y= ax^2+bx+c(a≠0)$ 的图象如下,根据图象解答下列问题.

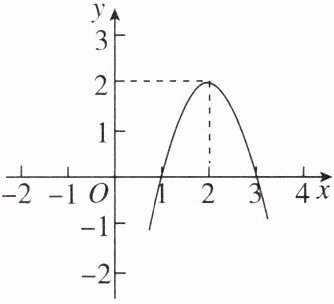
(1) 写出方程 $ax^2+bx+c= 0$ 的两个根.
(2) 分别写出不等式 $ax^2+bx+c＞0$ 的解集和 $ax^2+bx+c＜0$ 的解集.
(3) 写出 $y$ 随 $x$ 的增大而减小时,自变量 $x$ 的取值范围.
(4) 写出方程 $ax^2+bx+c= 2$ 的解.

答案：
(1)从题干图中可以看出抛物线与x轴交于(1,0)和(3,0)两点,
∴方程ax²+bx+c=0的两个根为x₁=1,x₂=3.
(2)从题干图中可以看出,当1＜x＜3时,y＞0;当x＜1或x＞3时,y＜0,
∴不等式ax²+bx+c＞0的解集为1＜x＜3,不等式ax²+bx+c＜0的解集为x＜1或x＞3.
(3)从题干图中可以看出对称轴为直线x=2,
∴当x≥2时,y随x的增大而减小.
(4)方程ax²+bx+c=2的解为x₁=x₂=2.