《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

1. 下列语句所描述的事件中,属于不可能事件的是 ( )

A.黄河入海流
B.大漠孤烟直
C.手可摘星辰
D.红豆生南国

答案： C

2. 下列事件属于必然事件的是 ( )

A.温岭明天会下雪
B.经过有交通信号灯的路口,遇到绿灯
C.足球队员在罚点球时,未进球
D.通常加热到 100℃时,水沸腾

答案： D

3. 老师从甲、乙、丙、丁四名同学中任选一人去学校劳动基地浇水,选中甲同学的概率是 ( )

A.$\frac{1}{5}$
B.$\frac{1}{4}$
C.$\frac{1}{3}$
D.$\frac{3}{4}$

答案： B

4. 抛掷一枚质地均匀、六个面上分别刻有 1 到 6 的点数的骰子,则下列事件中,发生可能性最小的是 ( )

A.向上一面的点数是 1
B.向上一面的点数比 3 小
C.向上一面的点数是偶数
D.向上一面的点数是 3 的倍数

答案： A

5. 从$-1,0,\sqrt{2},-0.3,\pi,\frac{1}{3}$中任意抽取一个数.下列事件中发生的概率最大的是 ( )

A.取到正数
B.取到非负数
C.取到无理数
D.取到分数

答案： B

6. 掷一枚质地均匀的骰子,向上一面的点数为 3 的概率是______.

答案： $\frac{1}{6}$

7. 某情报站有 A,B,C,D 四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种,如果第 1 周使用 A 种密码,那么第 3 周也使用 A 种密码的概率是______.

答案： $\frac{1}{3}$

8. 下图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.(注：频率$=\frac{钉尖向上的次数}{投掷次数}$)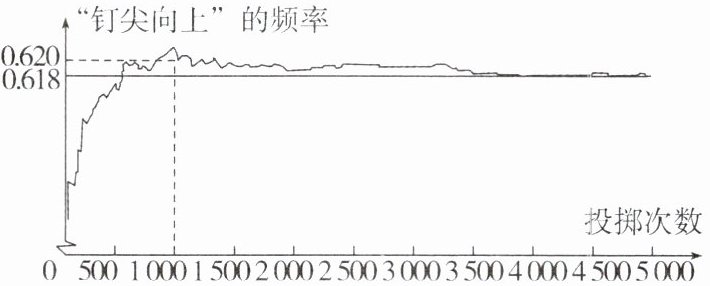
下面有四个推断：
①当投掷次数是 600 时,计算机记录“钉尖向上”的次数是 400,所以“钉尖向上”的概率是 0.667.
②随着试验次数的增加,“钉尖向上”的频率总在 0.618 附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是 0.618.
③若再次用计算机模拟试验,则当投掷次数为 1000 时,“钉尖向上”的概率一定是 0.620.
④若再次用计算机模拟试验,则当投掷次数为 1000 时,“钉尖向上”的情况一定高于 500 次.
其中合理的是______.(填序号)

答案： ②