《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

1. 下列条件中能确定一个圆的是( )

A.已知圆心
B.已知半径
C.过三个已知点
D.过三角形的三个顶点

答案： D

2. 三角形的外心具有的性质是 ( )

A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内

答案： B

3. 如图,点 A,B,C 均在 6×6 的正方形网格的格点上,过 A,B,C 三点的圆除经过 A,B,C 三点外还能经过的格点有( )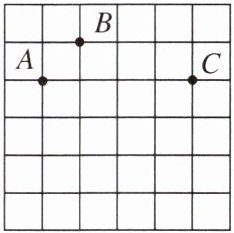

A.2个
B.3个
C.4个
D.5个

答案： D

4. 在 $Rt\triangle ABC$ 中,$AB= 6$,$BC= 8$,那么这个三角形的外接圆直径是 ( )

A.5
B.10
C.5 或 4
D.10 或 8

答案： D

5. 下列命题中,正确的是 ( )

A.三点确定一个圆
B.圆有且只有一个内接三角形
C.三角形有且只有一个外接圆
D.菱形的四个顶点在同一个圆上

答案： C

6. 直角三角形的外心是______；若三角形的外心在三角形的外部,则这个三角形是______三角形.

答案： 斜边的中点 钝角

7. 如图,点 A,B,C 均在直线 $l$ 上,点 P 在直线 $l$ 外,则经过其中任意三个点,最多可画出圆的个数为______.

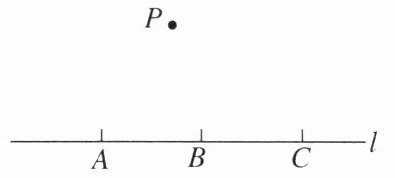
答案： 3

8. 聪聪用铅笔在一张白纸上点了一点 O,然后拿起一把直尺,平放在纸上,让尺子的一条边贴住这个点 O,用铅笔沿直尺的另一边画了一条直线(如图 1),聪聪又把尺子换了位置,用刚才的方法接着画出了第二条直线、第三条直线……(如图 2),慢慢地中间出现了一个圆(如图 3).请说说聪聪用直尺画圆的道理是______.

答案： 到定点的距离等于定长的点都在同一个圆上

9. 已知线段 $AB= 6\ cm$.
(1)画半径为 $4\ cm$ 的圆,使它经过 A,B 两点,这样的圆能画几个？
(2)画半径为 $3\ cm$ 的圆,使它经过 A,B 两点,这样的圆能画几个？
(3)画半径为 $2\ cm$ 的圆,使它经过 A,B 两点,这样的圆能画几个？

答案：
解:
(1)这样的圆能画2个,如图1.
作AB的垂直平分线l,再以点A为圆心、4 cm为半径作弧交l于O₁和O₂,然后分别以O₁和O₂为圆心、4 cm为半径作圆,则$\odot O_{1}$和$\odot O_{2}$为所求.

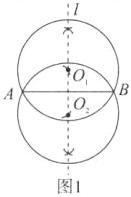
(2)这样的圆能画1个,如图2.
作AB的垂直平分线l,交AB于点O,然后以O为圆心、3 cm为半径作圆,则$\odot O$为所求.

(3)这样的圆不存在.