《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

1. 一个圆弧形蔬菜大棚的剖面如图所示,已知$AB= 16\ m$,半径$OA= 10\ m$,则高度$CD$的长为( )


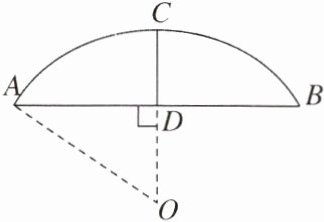
A.$2\ m$
B.$4\ m$
C.$6\ m$
D.$8\ m$

答案： B

2. 如图,$\odot O的弦AB垂直平分半径OC$,垂足为$D$,若$CD= \frac{\sqrt{2}}{2}$,则$AB$的长为( )


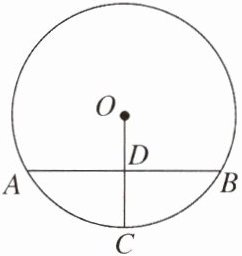
A.$\frac{\sqrt{10}}{2}$
B.$\sqrt{10}$
C.$\frac{\sqrt{6}}{2}$
D.$\sqrt{6}$

答案： D

3. 如图,$\odot O是等边三角形ABC$的外接圆,若$AB= 3$,则$\odot O$的半径是( )


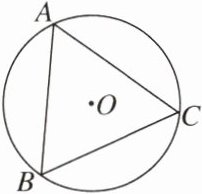
A.$\frac{3}{2}$
B.$\frac{\sqrt{3}}{2}$
C.$\sqrt{3}$
D.$\frac{5}{2}$

答案： C

4. 一块圆形玻璃镜面碎成了几块,其中一块如下图所示,测得弦$AB$长20厘米,弓形高$CD$为2厘米,则镜面半径为______厘米.

答案： 26

5. 如图,这是某圆弧形石拱桥的侧面图,桥的跨径$AB= 18\ m$,拱高$CD= 5\ m$,则拱桥的半径为______m.

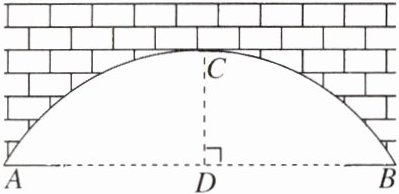
答案： $\frac{53}{5}$ 【解析】设$\overset{\frown}{AB}$所在圆的圆心为O，半径为r，由题意可知AB=18 m，OD=(r - 5)m，
∵OC⊥AB，
∴∠ADO=90°，AD=BD= $\frac{1}{2}$AB=9 m，则由勾股定理得OA²=AD²+OD²，即r²=9²+(r - 5)²，解得r= $\frac{53}{5}$.

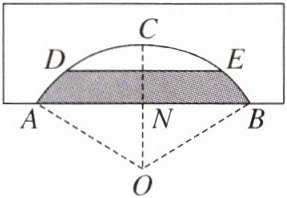
6. 如图,有一座圆弧形拱桥,桥下水面宽$AB为16\ m$,拱高$CN为4\ m$.
(1)求桥拱的半径.
(2)此桥的安全限度是拱顶$C点距离水面不得小于1.5\ m$,若大雨过后,洪水泛滥到水面宽度$DE为12\ m$时,是否需要采取紧急措施？请说明理由.

答案：

(1)求桥拱的半径.解：如图，半径OC⊥AB，OC⊥DE.设桥拱的半径是r m，
∵OC⊥AB，
∴AN= $\frac{1}{2}$AB= $\frac{1}{2}$×16=8(m).
∵拱高CN为4 m，
∴ON=(r - 4)m.
∵OA²=ON²+AN²，
∴r²=(r - 4)²+8²，
∴r=10，
∴桥拱的半径是10 m.
(2)此桥的安全限度是拱顶C点距离水面不得小于1.5 m，若大雨过后，洪水泛滥到水面宽度DE为12 m时，是否需要采取紧急措施？请说明理由.解：不需要采取紧急措施，理由如下：如图，连结OD.设CO与DE相交于点M.
∵CO⊥DE，
∴DM= $\frac{1}{2}$DE= $\frac{1}{2}$×12=6(m)，
∴OM= $\sqrt{OD^2 - DM^2}$= $\sqrt{10^2 - 6^2}$=8(m).
∵CM=OC - OM=10 - 8=2(m)，且2 m＞1.5 m，
∴不需要采取紧急措施.