《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

【例1】如图,在$\triangle ABC$中,D为BC的中点,以D为圆心,BD长为半径画弧,交AC于点E,若$\angle A= 60°$,$\angle ABC= 100°$,$BC= 4$,则扇形BDE的面积为______.

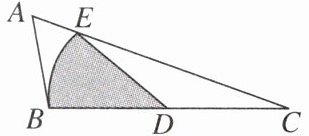
答案： $\frac{4\pi}{9}$

【变式】如图,已知在$\triangle ABC$中,$\angle A= 72°$,$BC= 10$,若以BC为直径作$\odot O$分别交AB,AC于点M,N,则图中阴影部分的面积为______.(结果保留$\pi$)

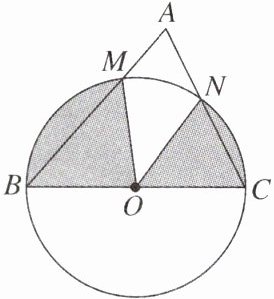
答案： $10\pi$ 【解析】$\because \angle A=72^{\circ },\angle A+\angle B+\angle C =180^{\circ },$$\therefore \angle B+\angle C=108^{\circ }.$
∵以 BC 为直径作$\odot O$分别交 AB,AC 于点 M,N,$\therefore OB=OM=OC=ON=\frac {1}{2}BC=5,$$\therefore \angle B=\angle OMB,\angle C=\angle ONC,$$\therefore \angle OMB+\angle ONC=\angle B+\angle C=108^{\circ },$$\therefore \angle BOM+\angle CON=180^{\circ }-(\angle B+\angle OMB)+180^{\circ }-(\angle C+\angle ONC)=360^{\circ }-(\angle B+\angle C)-(\angle OMB+\angle ONC)=144^{\circ },$$\therefore S_{阴影}=S_{扇形BOM}+S_{扇形CON}=\frac {(\angle BOM+\angle CON)\pi × 5^{2}}{360}=\frac {144\pi × 25}{360}=10\pi .$

【例2】如图,在扇形AOB中,$OA= 1$,P为OB上的一个动点,将$\triangle OAP$沿AP折叠,当点O的对应点Q落在$\overset{\frown}{AB}$上时,图中阴影部分的面积为______.

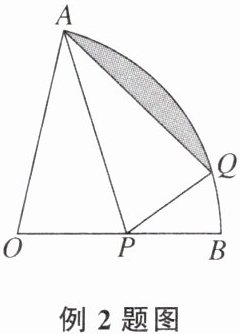
答案：
$\frac {\pi }{6}-\frac {\sqrt {3}}{4}$【解析】如图,连结 OQ 交 AP 于点 C,
∵将$\triangle OAP$沿 AP 折叠得到$\triangle QAP$,且 Q 点落在$\widehat {AB}$上，$\therefore AP⊥OQ,OC=QC=\frac {1}{2}OQ=\frac {1}{2}OA=\frac {1}{2},$$\therefore \angle ACO=90^{\circ },\angle OAC=30^{\circ },$$\therefore \angle AOQ=90^{\circ }-30^{\circ }=60^{\circ },AC=\sqrt {OA^{2}-OC^{2}}=\sqrt {1-\frac {1}{4}}=\frac {\sqrt {3}}{2},$$\therefore S_{阴影}=S_{扇形AOQ}-S_{\triangle AOQ}=\frac {60\pi × 1^{2}}{360}-\frac {1}{2}× 1× \frac {\sqrt {3}}{2}=\frac {\pi }{6}-\frac {\sqrt {3}}{4}.$

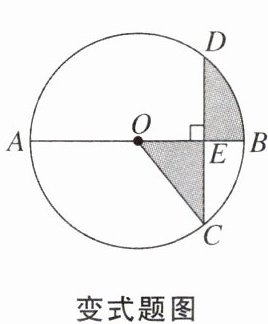
【变式】如图,AB是$\odot O$的直径,CD为$\odot O$的弦,$AB\perp CD$于点E.已知$CD= 4\sqrt{3}$,$AE= 6$,则阴影部分的面积为______.

答案： $\frac {8}{3}\pi$

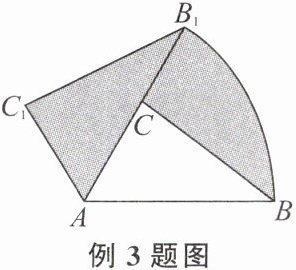
【例3】如图,在$\triangle ABC$中,$AB= 2$,现将$\triangle ABC$绕点A逆时针旋转$60°得到\triangle AB_1C_1$,点C在$AB_1$上,则图中阴影部分的面积为( )

A.$\frac{3}{4}\pi$
B.$\frac{4}{3}\pi$
C.$\frac{3}{2}\pi$
D.$\frac{2}{3}\pi$

答案： D

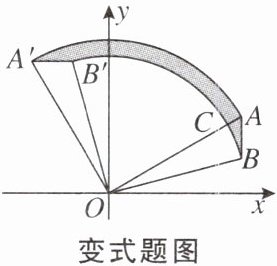
【变式】如图,已知点$A(2\sqrt{3},2)$,$B(2\sqrt{3},1)$,将$\triangle AOB$绕着点O逆时针旋转,使点A旋转到点$A'(-2,2\sqrt{3})$的位置,则图中阴影部分的面积为______.

答案： $\frac {3}{4}\pi$

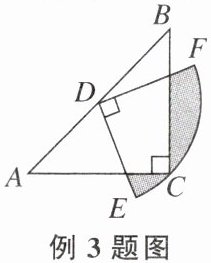
【例4】如图,在$\triangle ABC$中,$CA= CB$,$\angle ACB= 90°$,$AB= 2$,D为AB的中点,以点D为圆心作圆心角为$90°$的扇形EDF,点C恰在$\overset{\frown}{EF}$上,则图中阴影部分的面积为______.

答案：
$\frac {\pi }{4}-\frac {1}{2}$【解析】如图,连结 CD,$\because CA=CB,\angle ACB=90^{\circ },\therefore \angle B=45^{\circ }.$
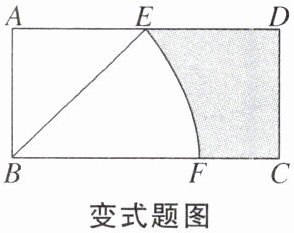
∵ D 为 AB 的中点,$\therefore DC=\frac {1}{2}AB=BD=1,$$CD⊥AB,\angle DCA=45^{\circ },$$\therefore \angle CDH=\angle BDG,\angle DCH=\angle B.$在$\triangle DCH$和$\triangle DBG$中,$\left\{\begin{array}{l} \angle CDH=\angle BDG\\ CD=BD\\ \angle DCH=\angle B\end{array}\right. $$\therefore \triangle DCH\cong \triangle DBG(ASA),$$\therefore S_{四边形DGCH}=S_{\triangle BDC}=\frac {1}{2}S_{\triangle ABC}=\frac {1}{2}× \frac {1}{2}AB\cdot CD=\frac {1}{4}× 2× 1=\frac {1}{2},$$\therefore S_{阴影}=S_{扇形EDF}-S_{四边形DGCH}=\frac {90\pi × 1^{2}}{360}-\frac {1}{2}=\frac {\pi }{4}-\frac {1}{2}.$

【变式】如图,在矩形ABCD中,$AB= \sqrt{2}$,BE平分$\angle ABC$交AD于点E,以B为圆心,BE长为半径画弧,交BC于点F.若点E为AD的中点,则图中阴影部分的面积为( )

A.$6-\frac{\pi}{4}$
B.$3-\frac{\pi}{4}$
C.$6-\frac{\pi}{2}$
D.$3-\frac{\pi}{2}$

答案： D