《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 在 Rt△ABC 中,∠C= 90°,a,b,c 分别是∠A,∠B,∠C 的对边.
(1)已知 $c= 2\sqrt{3}$,$b= \sqrt{6}$,求∠A.
(2)已知 c= 12,$\sin A= \frac{1}{2}$,求 b.

答案：
(1)$\because \cos A = \frac{b}{c} = \frac{\sqrt{6}}{2\sqrt{3}} = \frac{\sqrt{2}}{2}$,$\therefore \angle A = 45^{\circ}$.
(2)$\because \sin A = \frac{1}{2} = \frac{a}{c} = \frac{a}{12}, \therefore a = 6$,$\therefore b = \sqrt{c^{2} - a^{2}} = 6\sqrt{3}$.

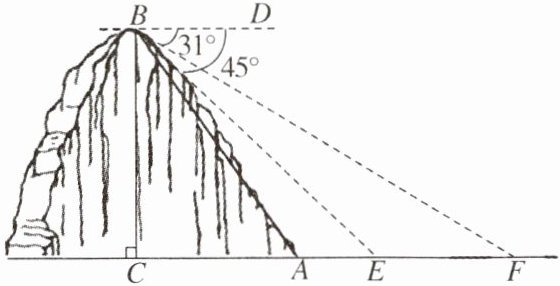
10. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥. 如图,河旁有一座小山,山高 BC= 80 m,点 C,A 与河岸 E,F 在同一水平线上,从山顶 B 处测得河岸 E 和对岸 F 的俯角分别为∠DBE= 45°,∠DBF= 31°. 若在此处建桥,求河宽 EF 的长.(结果精确到 1 m,参考数据：sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)

答案： 解:在$Rt\triangle BCE$中,$BC = 80$m,$\angle BEC = \angle DBE = 45^{\circ}$,$\therefore \angle CBE = 45^{\circ}$,$\therefore \angle BEC = \angle CBE = 45^{\circ}$,$\therefore CE = BC = 80$m.在$Rt\triangle BCF$中,$BC = 80$m,$\angle BFC = \angle DBF = 31^{\circ}$,$\tan\angle BFC = \frac{BC}{CF}$,即$\frac{80}{CF} \approx 0.60$,$\therefore CF \approx 133.3$(m),$\therefore EF = CF - CE \approx 133.3 - 80 = 53.3 \approx 53$(m).答:河宽EF的长约为53m.

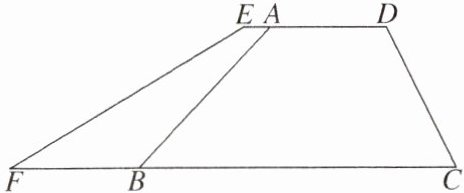
11. 某村准备对水库一段长 100 m 的堤坝进行改造. 改造前,背水坡坡面 AB 的坡比 i= 1:1,改造后坡面 EF 的坡比变为 2:3,坝顶加宽 1 m(AE= 1 m),已知原背水坡 AB 的长为 8 m.
(1)求改造后背水坡 EF 的长.
(2)求所需土石方的体积.(结果精确到 1 m^3,参考数据：$\sqrt{2}\approx1.414$)

答案：

(1)如图,分别过点A,E作$AQ\perp BC$于点Q,$EP\perp BC$于点P. 在$Rt\triangle ABQ$中,$\because$背水坡坡面AB的坡比$i = 1:1$,$\therefore AQ = BQ = 4\sqrt{2}$m,在$Rt\triangle EFP$中,$\because$改造后坡面EF的坡比变为2:3,$EP = AQ = 4\sqrt{2}$m,$\therefore FP = 6\sqrt{2}$m,$\therefore EF = \sqrt{PE^{2} + PF^{2}} = 2\sqrt{26}$m,答:改造后背水坡EF的长为$2\sqrt{26}$m.
(2)在$Rt\triangle EFP$中,$\because$改造后坡面EF的坡比变为2:3,$FP = 6\sqrt{2}$m,$\therefore FB = FQ - BQ = FP + PQ - BQ = 6\sqrt{2} + 1 - 4\sqrt{2} = (2\sqrt{2} + 1)$m,$\therefore$土石方的体积$ = \frac{1}{2}× (1 + 2\sqrt{2} + 1)× 4\sqrt{2}× 100 = 100× (8 + 4\sqrt{2}) \approx 1366$($m^{3}$).答:所需土石方的体积约为$1366m^{3}$.