《2025年初中同步练习册七年级数学上册北师大版北京师范大学出版社》

7. 若$-3x^{2m}y^{3}与2x^{4}y^{n}$是同类项,则$|m-n|$的值是(B)。
A.0
B.1
C.7
D.-1

答案： B

8. 已知$m-n= 100$,$x+y= -1$,则代数式$(n+x)-(m-y)$的值是 -101。

答案： -101

9. 已知$(a+2)^{2}+|b-3|= 0$,求$\frac{1}{3}(9ab^{2}-3)+(7a^{2}b-2)+2(ab^{2}-1)-2a^{2}b$的值。

答案： -35

10. 已知$A= x^{3}+6x-9$,$B= -x^{3}-2x^{2}+4x-6$,求$2A-3B$。

答案： $5x^{3}+6x^{2}$

11. 如图,用若干根相同的小棒摆正六边形,其中正六边形的每条边需要一根小棒。
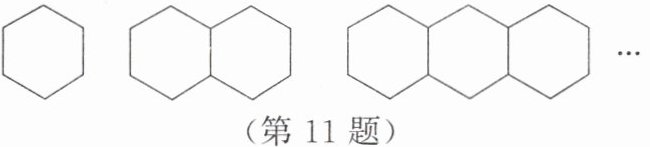
(1) 摆1个正六边形需要 6 根小棒,摆2个正六边形需要 ______11 根小棒,摆3个正六边形需要 ______16 根小棒。
(2) 照这样摆下去：
① 摆$n$个正六边形需要几根小棒？当$n= 200$时,需要几根小棒？
② 181根小棒可以摆多少个正六边形？

答案： 解:
(1)6 11 16
(2)①摆n个正六边形需要$(5n+1)$根小棒;当$n=200$时,需要$5× 200+1=1001$(根)小棒。
②当$5n+1=181$时,$n=(181-1)÷ 5=36$,即可以摆36个正六边形。

12. 用同样规格的黑、白两色正方形瓷砖铺设长方形地面,请观察下图,并探究和解决下列问题：
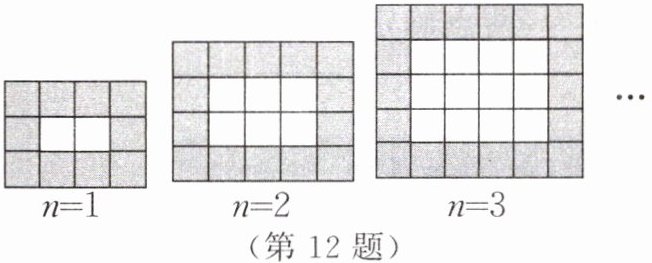
(1) 第$n$个图形中,每一行有 $(n+3)$块瓷砖,每一列有 ______ $(n+2)$块瓷砖。
(2) 在铺设第$n$个图形时,共用多少块瓷砖？
(3) 如果每块黑瓷砖4元,每块白瓷砖3元,铺设第10个图形时,共需多少钱购买瓷砖？

答案： 解:
(1)$(n+3)$ $(n+2)$
(2)$(n+3)(n+2)$块
(3)白瓷砖需$n(n+1)$块,当$n=10$时,白瓷砖需$10× 11=110$(块),黑瓷砖需$13× 12-110=156-110=46$(块)。共需$110× 3+46× 4=514$(元)购买瓷砖。