第31页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
9. 如图所示的是按一定规律排列的一组数据,任意圈出 $ 3 × 3 $ 个数。

(1) 计算:$ (-4)+18+(-32)= $
(2) 再任意圈出 $ 3 × 3 $ 个数,(1)中的结论还成立吗?
(1)结论:对角线上三个数之和是中间数的相反数。
(2)如图,圈出3×3个数,26+(-40)+54=40,30+(-40)+50=40,
(1)中的结论仍然成立。(答案不唯一)2 -4 6 -8 10 -1214 -16 18 -20 22 -2426 -28 30 -32 34 -3638 -40 42 -44 46 -4850 -52 54 -56 58 -60(第9题)

(1) 计算:$ (-4)+18+(-32)= $
-18
,$ (-28)+18+(-8)= $-18
。你能得出什么结论?(2) 再任意圈出 $ 3 × 3 $ 个数,(1)中的结论还成立吗?
(1)结论:对角线上三个数之和是中间数的相反数。
(2)如图,圈出3×3个数,26+(-40)+54=40,30+(-40)+50=40,
(1)中的结论仍然成立。(答案不唯一)2 -4 6 -8 10 -1214 -16 18 -20 22 -2426 -28 30 -32 34 -3638 -40 42 -44 46 -4850 -52 54 -56 58 -60(第9题)
答案:
解:
(1)-18 -18 结论:对角线上三个数之和是中间数的相反数。
(2)如图,圈出3×3个数,26+(-40)+54=40,30+(-40)+50=40,
(1)中的结论仍然成立。(答案不唯一)2 -4 6 -8 10 -1214 -16 18 -20 22 -2426 -28 30 -32 34 -3638 -40 42 -44 46 -4850 -52 54 -56 58 -60(第9题)
(1)-18 -18 结论:对角线上三个数之和是中间数的相反数。
(2)如图,圈出3×3个数,26+(-40)+54=40,30+(-40)+50=40,
(1)中的结论仍然成立。(答案不唯一)2 -4 6 -8 10 -1214 -16 18 -20 22 -2426 -28 30 -32 34 -3638 -40 42 -44 46 -4850 -52 54 -56 58 -60(第9题)
10. 【数学游戏】小彬和晓丽做抽卡片游戏,游戏规则如下:
(1) 每人抽取 $ 4 $ 张卡片,如果抽到圆圈卡片,那么加上卡片上的数;如果抽到阴影卡片,那么减去卡片上的数。
(2) 比较两人所抽 $ 4 $ 张卡片的计算结果,结果大的为胜者。
小彬抽到了如图①所示的 $ 4 $ 张卡片:
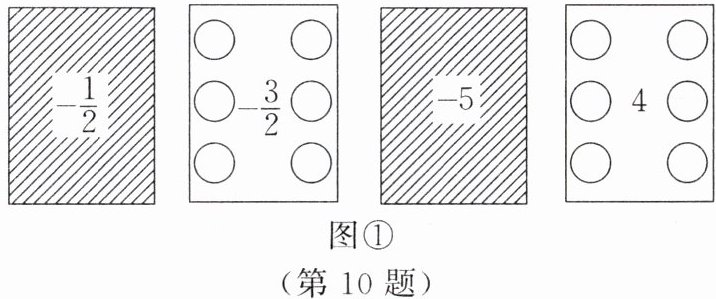
晓丽抽到了如图②所示的 $ 4 $ 张卡片:

获胜的是谁?
(1) 每人抽取 $ 4 $ 张卡片,如果抽到圆圈卡片,那么加上卡片上的数;如果抽到阴影卡片,那么减去卡片上的数。
(2) 比较两人所抽 $ 4 $ 张卡片的计算结果,结果大的为胜者。
小彬抽到了如图①所示的 $ 4 $ 张卡片:

晓丽抽到了如图②所示的 $ 4 $ 张卡片:

获胜的是谁?
答案:
解:小彬的结果是-(-$\frac{1}{2}$)+(-$\frac{3}{2}$)-(-5)+4=$\frac{1}{2}$-$\frac{3}{2}$+5+4=8。晓丽的结果是(-$\frac{1}{3}$)-(-$\frac{7}{6}$)-0+5=-$\frac{1}{3}$+$\frac{7}{6}$-0+5=5$\frac{5}{6}$。因为8>5$\frac{5}{6}$,所以小彬获胜。
11. 【数学游戏】将 $ -2 $,$ -1 $,$ 0 $,$ 1 $,$ 2 $,$ 3 $,$ 4 $,$ 5 $,$ 6 $,$ 7 $ 这 $ 10 $ 个数分别填在如图所示的五角星每两条线的交点处(每个交点处只填写一个数)。将每一条线上的四个数相加共得 $ 5 $ 个数,设为 $ a_1 $,$ a_2 $,$ a_3 $,$ a_4 $,$ a_5 $,求 $ \frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5) $ 的值。若交换其中任何两数的位置后,$ \frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5) $ 的值是否改变?请说明理由。


答案:
五角星有5条线,每条线上4个数,每个交点处的数被两条线共用。这10个数的和为$-2 + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 = 25$。$a_1 + a_2 + a_3 + a_4 + a_5$等于这10个数的和的2倍,即$2×25 = 50$,所以$\frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5)=\frac{1}{2}×50 = 25$。交换任何两数位置,这10个数的总和不变,故$\frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5)$的值不改变。
25,不改变,理由:因为每个数都被两条线共用,$a_1 + a_2 + a_3 + a_4 + a_5$等于这10个数和的2倍,交换两数位置不改变10个数的和,所以$\frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5)$的值不变。
25,不改变,理由:因为每个数都被两条线共用,$a_1 + a_2 + a_3 + a_4 + a_5$等于这10个数和的2倍,交换两数位置不改变10个数的和,所以$\frac{1}{2}(a_1 + a_2 + a_3 + a_4 + a_5)$的值不变。
查看更多完整答案,请扫码查看


