《2025年初中同步练习册七年级数学上册北师大版北京师范大学出版社》

10. 小华做这样一道题：“计算$\vert (-4)-*\vert$。”其中$*$表示被墨水污染看不清的一个数,他翻开后面的答案得知该题的结果是$7$,那么$*$表示的数是3 或-11。

答案： 3 或-11

11. 计算：
(1)$(+18)-(+6)-(+19)-(-20)-(-5)$；
(2)$(+4.25)-(+3.6)-(-3.75)-(+1.4)$。

答案： 解:
(1)原式=18-6-19+20+5 =12-19+20+5 =(-7)+20+5 =13+5 =18。
(2)原式=4.25+(-3.6)+3.75+(-1.4) =(4.25+3.75)+[(-3.6)+(-1.4)] =8+[-(3.6+1.4)] =8+(-5) =3。

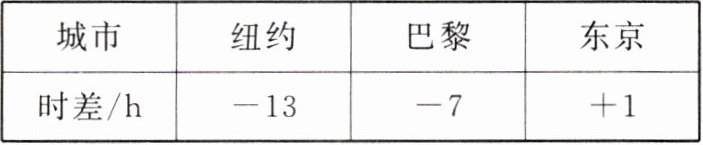
12. 【数学应用】下表列出了国外几个城市与北京的时差。
|城市|纽约|巴黎|东京|
|时差/h|$-13$|$-7$|$+1$|

(1)如果现在是北京时间上午$8:00$,那么此时东京时间是多少？
(2)某日北京时间为$15:00$,小明想给在纽约的朋友打电话,你认为合适吗？

答案： 分析:首先弄清时差的含义,带正号的数表示同一时刻比北京时间早的时数,带负号的数表示同一时刻比北京时间晚的时数。 解:
(1)因为8+1=9,所以东京时间是上午9:00。
(2)15-13=2。 北京时间是15:00,纽约时间是凌晨2:00,显然小明这时打电话是不合适的。

13. 【数学应用】红星队在$4$场足球赛中的成绩如下：第一场$3:1$胜,第二场$2:3$负,第三场$0:0$平,第四场$2:5$负。红星队在这$4$场比赛中总的净胜球数是多少？(注：红星队若$2:0$胜,则净胜球个数为$2-0= 2$；若$0:2$负,则净胜球个数为$0-2= -2$)

答案： 解:由题知(3-1)+(2-3)+(0-0)+(2-5)=-2。

14. 【综合与实践】阅读下列式子：
$\frac{1}{1×2}= 1-\frac{1}{2}$；
$\frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$；
$\frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$；
…
则(1)$\frac{1}{n(n+1)}=$$\frac{1}{n}-\frac{1}{n+1}$；
(2)计算：$\frac{1}{2}-\frac{1}{6}-\frac{1}{12}-\frac{1}{20}-\frac{1}{30}-\frac{1}{42}$；
(3)计算：$\frac{1}{1×5}+\frac{1}{5×9}+\frac{1}{9×13}+…+\frac{1}{2021×2025}$。
(2)原式=$\frac{1}{2}-(\frac{1}{2}-\frac{1}{3})-(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})-(\frac{1}{5}-\frac{1}{6})-(\frac{1}{6}-\frac{1}{7})=\frac{1}{7}$。
(3)原式=$\frac{1}{4}×(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\cdots+\frac{1}{2021}-\frac{1}{2025})$
=$\frac{1}{4}×(1-\frac{1}{2025})$
=$\frac{1}{4}×\frac{2024}{2025}$
=$\frac{506}{2025}$。

答案： 解:
(1)$\frac{1}{n}-\frac{1}{n+1}$
(2)原式=$\frac{1}{2}-(\frac{1}{2}-\frac{1}{3})-(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})-(\frac{1}{5}-\frac{1}{6})-(\frac{1}{6}-\frac{1}{7})=\frac{1}{7}$。
(3)原式=$\frac{1}{4}×(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\cdots+\frac{1}{2021}-\frac{1}{2025})$ =$\frac{1}{4}×(1-\frac{1}{2025})$ =$\frac{1}{4}×\frac{2024}{2025}$ =$\frac{506}{2025}$。