《2025年初中同步练习册七年级数学上册北师大版北京师范大学出版社》

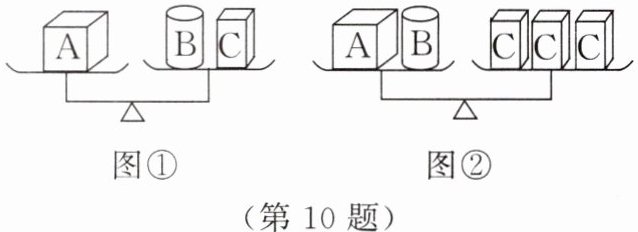
10. 如图,在图①所示的天平上,物体 A 的质量等于物体 B 的质量加物体 C 的质量；在图②所示的天平上,物体 A 的质量加物体 B 的质量等于 3 个物体 C 的质量。由此可知,1 个物体 A 的质量与(B)个物体 C 的质量相等。

A.1
B.2
C.3
D.4

答案： B

11. 在天平的左边放 3 枚硬币和 12g 砝码,右边放 5 枚硬币和 4g 砝码,天平恰好平衡。已知所有硬币的质量都相同,如果设 1 枚硬币的质量为$x$g,可列出方程为(A)。
A.$3x + 12 = 5x + 4$
B.$3x - 12 = 5x - 4$
C.$3x + 12 = 5x - 4$
D.$3x - 12 = 5x + 4$

答案： A

12. 阅读小明利用等式的基本性质解方程的过程,指出他错在哪一步,为什么？
$2(y + 2) - 3 = 5(y + 2) - 3$。
方程两边都加 3,得$2(y + 2) = 5(y + 2)$。①
方程两边都除以$y + 2$,得$2 = 5$。②

答案： 解:错在第②步。因为不能确定y+2的值是不是0,所以方程两边不能同时除以y+2。

13.【综合与实践】根据等式的基本性质,回答下列问题：
(1)从$ab = bc能否得到a = c$？为什么？
(2)从$\frac{a}{b}= \frac{c}{b}能否得到a = c$？为什么？
(3)从$ab = 1能否得到a + 1= \frac{1}{b}+1$？为什么？

答案： 解:
(1)不一定。当b≠0时,根据等式的基本性质可得a=c;当b=0时,a不一定等于c。
(2)能得到。由题意,知b≠0,根据等式的基本性质,在$\frac{a}{b}=\frac{c}{b}$的两边都乘b,得a=c。
(3)能得到。显然b≠0,根据等式的基本性质,在ab=1的两边都除以b,得$a=\frac{1}{b},$再根据等式的基本性质,在$a=\frac{1}{b}$两边都加1,得$a+1=\frac{1}{b}+1。$

14.【数学文化】阅读下列材料,解决相应问题：
中国古代数学,和天文学以及其他许多科学技术一样,也取得了极其辉煌的成就。可以毫不夸张地说,明代中叶以前,在数学的许多分支领域里,中国一直处于遥遥领先的地位。中国古代的数学家写下了许多数学著作。许多具有世界意义的成就正是因为有了这些古算书才流传下来。
我国流传着许多趣味算题,它们多以顺口溜的形式表述。请大家看这样一个数学问题：一群老头去赶集,半路买了一堆梨,一人一个多一梨,一人两个少两梨,多少老头多少梨？
(1)如果我们设有$x$个老头,可以得到关于$x$的等式为x+1=2x-2。
(2)利用等式的基本性质求出,共有3个老头、4个梨。

答案：
(1)x+1=2x-2
(2)3 4