第71页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
10. 若 $A$,$B$,$C$ 三点在同一直线上,且线段 $AB = 4\ cm$,$BC = 2\ cm$,则 $A$,$C$ 两点之间的距离为(
A.$2\ cm$
B.$6\ cm$
C.$2\ cm$ 或 $6\ cm$
D.无法确定
C
)。A.$2\ cm$
B.$6\ cm$
C.$2\ cm$ 或 $6\ cm$
D.无法确定
答案:
C
11. 已知点 $M$ 在线段 $AB$ 上,在 ①$AB = 2AM$,②$BM= \frac{1}{2}AB$,③$AM = BM$,④$AM + BM = AB$ 四个式子中,能说明 $M$ 是线段 $AB$ 的中点的式子有(
A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$4$ 个
C
)。A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$4$ 个
答案:
C
12. 已知 $A$,$B$,$C$ 三点在同一条直线上,点 $M$,$N$ 分别为线段 $AB$,$BC$ 的中点,且 $AB = 50$,$BC = 20$,求 $MN$ 的长。
答案:
解:因为点M,N分别为AB,BC的中点,所以$BM=\frac{1}{2}AB=25$,$BN=\frac{1}{2}BC=10$。如图①,$MN=BM+BN=25+10=35$;如图②,$MN=BM - BN=25 - 10=15$。综上,MN的长为35或15。
解:因为点M,N分别为AB,BC的中点,所以$BM=\frac{1}{2}AB=25$,$BN=\frac{1}{2}BC=10$。如图①,$MN=BM+BN=25+10=35$;如图②,$MN=BM - BN=25 - 10=15$。综上,MN的长为35或15。

13.【数学应用】已知平面上四点 $A$,$B$,$C$,$D$(每三点都不在一条直线上)。
(1) 经过这四点最多能确定
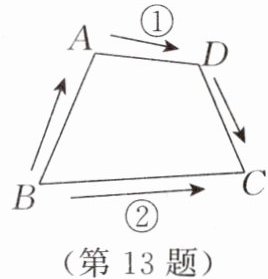
(2) 如图,现用这四点表示公园里的四个地方,如果点 $B$,$C$ 在公园里湖对岸两处,$A$,$D$ 在湖面上,要从 $B$ 到 $C$ 筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
(1) 经过这四点最多能确定
6
条直线。(2) 如图,现用这四点表示公园里的四个地方,如果点 $B$,$C$ 在公园里湖对岸两处,$A$,$D$ 在湖面上,要从 $B$ 到 $C$ 筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?

解:从节省材料的角度考虑,应选择题图中路线②;如果有人想在桥上较长时间观赏湖面风光,应选择题图中路线①。因为两点之间线段最短,所以路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光。(答案合理即可)
答案:
(1)6
(2)解:从节省材料的角度考虑,应选择题图中路线②;如果有人想在桥上较长时间观赏湖面风光,应选择题图中路线①。因为两点之间线段最短,所以路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光。(答案合理即可)
(1)6
(2)解:从节省材料的角度考虑,应选择题图中路线②;如果有人想在桥上较长时间观赏湖面风光,应选择题图中路线①。因为两点之间线段最短,所以路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光。(答案合理即可)
14.【综合与实践】如图,$A$,$B$,$C$ 是一条公路上的三个村庄,$A$,$B$ 间的路程为 $100\ km$,$A$,$C$ 间的路程为 $40\ km$。现计划在 $A$,$B$ 之间建一个车站 $P$,设 $P$,$C$ 之间的路程为 $x\ km$。
(1) 用含 $x$ 的代数式表示车站到三个村庄的路程之和。
(2) 若路程之和为 $102\ km$,则车站应建在何处?
(3) 若要使车站到三个村庄的路程总和最小,则车站应建在何处?路程总和的最小值是多少?

(1) 用含 $x$ 的代数式表示车站到三个村庄的路程之和。
(2) 若路程之和为 $102\ km$,则车站应建在何处?
(3) 若要使车站到三个村庄的路程总和最小,则车站应建在何处?路程总和的最小值是多少?

答案:
1. (1)
已知$AP=(40 + x)km$,$BP=(100-(40 + x))km=(60 - x)km$,$PC = xkm$。
则路程之和$S=AP + BP+PC=(40 + x)+(60 - x)+x$。
化简$S=(40 + 60)+(x - x)+x=(100 + x)km$。
2. (2)
当$S = 102km$时,即$100 + x=102$。
解方程$x=102 - 100=2$。
所以车站建在$C$两侧$2km$处(当$x = 2$时,若$P$在$C$右侧,$AP=40 + 2=42km$,$BP=60-2 = 58km$;若$P$在$C$左侧,$AP=40-2 = 38km$,$BP=60 + 2=62km$)。
3. (3)
因为$S=100 + x$,$x\geqslant0$。
根据一次函数$y = kx + b$(这里$k = 1\gt0$,$b = 100$)的性质,$y$随$x$的增大而增大。
所以当$x = 0$时,$S$取得最小值。
此时$S_{min}=100km$,车站建在$C$处。
综上,(1)路程之和为$(100 + x)km$;(2)车站建在$C$两侧$2km$处;(3)车站建在$C$处,路程总和最小值是$100km$。
已知$AP=(40 + x)km$,$BP=(100-(40 + x))km=(60 - x)km$,$PC = xkm$。
则路程之和$S=AP + BP+PC=(40 + x)+(60 - x)+x$。
化简$S=(40 + 60)+(x - x)+x=(100 + x)km$。
2. (2)
当$S = 102km$时,即$100 + x=102$。
解方程$x=102 - 100=2$。
所以车站建在$C$两侧$2km$处(当$x = 2$时,若$P$在$C$右侧,$AP=40 + 2=42km$,$BP=60-2 = 58km$;若$P$在$C$左侧,$AP=40-2 = 38km$,$BP=60 + 2=62km$)。
3. (3)
因为$S=100 + x$,$x\geqslant0$。
根据一次函数$y = kx + b$(这里$k = 1\gt0$,$b = 100$)的性质,$y$随$x$的增大而增大。
所以当$x = 0$时,$S$取得最小值。
此时$S_{min}=100km$,车站建在$C$处。
综上,(1)路程之和为$(100 + x)km$;(2)车站建在$C$两侧$2km$处;(3)车站建在$C$处,路程总和最小值是$100km$。
查看更多完整答案,请扫码查看


