《2025年顶尖课课练七年级数学上册人教版》

14. 如图4.2.2 - 1，两种长方形铝合金窗框，已知窗框的宽都是$a$m，长都是$b$m.一用户需A型窗框$2$个、B型窗框$4$个.

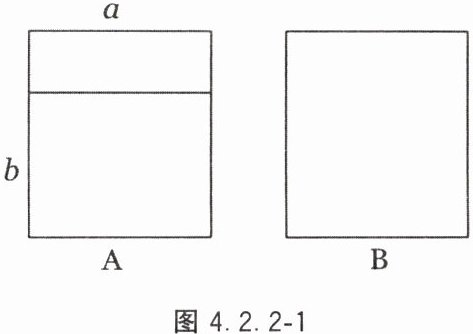
（1）用含$a$，$b$的式子表示共需铝合金的长度（窗框本身的宽度忽略不计）；
（2）若$1$m铝合金的平均费用为$50$元，求当$a = 1.5$，$b = 2.5$时，（1）中铝合金窗框的总费用.

答案： （1）（$14a+12b$）m （2）2550 元

15. 将式子$4x+(3x - x)=4x + 3x - x$，$4x-(3x - x)=4x - 3x + x$分别反过来，你将得到两个怎样的等式？
（1）比较你得到的等式，你能总结出添括号的法则吗？
（2）根据上面你总结的添括号法则，不改变多项式$-3x^{5}-4x^{2}+3x^{3}-2$的值，把它的后两项分别放在：
①前面带有“$+$”号的括号里；
②前面带有“$-$”号的括号里.
]

答案： （1）将式子反过来得：$4x + 3x - x = 4x + (3x - x)$；$4x - 3x + x = 4x - (3x - x)$。
添括号法则：添括号时，如果括号前面是正号，括到括号里的各项都不变符号；如果括号前面是负号，括到括号里的各项都改变符号。
（2）①$-3x^{5}-4x^{2}+(3x^{3}-2)$；
②$-3x^{5}-4x^{2}-(-3x^{3}+2)$。

1. $3ab$减去$-2ab$可列式为3ab-(-2ab)，结果为5ab。

答案： 3ab-(-2ab) 5ab

2. 下列运算中，结果正确的是(D)。

A.$4 + 5ab = 9ab$
B.$6xy - x = 6y$
C.$6a^{3}+4a^{5}=10a^{9}$
D.$8a^{2}b - 8ba^{2}=0$

答案： D

3. 多项式$3a + 2b$与$-5b + 2a$的和为5a-3b。

答案： 5a-3b

4. 已知一个多项式与$3x^{2}+9x$的和为$3x^{2}+4x - 1$，则这个多项式是(A)。

A.$-5x - 1$
B.$5x + 1$
C.$-13x - 1$
D.$13x + 1$

答案： A

5. 减去$-3x$等于$5x^{2}-3x - 5$的多项式是5x²-6x-5。

答案： 5x²-6x-5

6. 若多项式$axy^{2}-\frac{1}{2}x$与$\frac{1}{4}x - bxy^{2}$的和是一个单项式，则$a$，$b$的关系是a=b。

答案： a=b

7. 化简：
（1）$-3x^{2}+(-4xy)-6xy - 2x^{2}$；
（2）$3a - b + 2(2b^{2}-a^{2})-2(-a^{2}+2b^{2})$；
（3）$\frac{1}{3}a - (\frac{1}{2}a - 4b - 6c)+3(-2c + 2b)$。

答案： （1）-5x²-10xy （2）3a-b （3）-$\frac{1}{6}a$+10b