第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10. 比较$-\frac{1}{2}$,$-\frac{1}{3}$,$\frac{1}{4}$的大小,结果为
$-\frac{1}{2}$
<$-\frac{1}{3}$
<$\frac{1}{4}$
.
答案:
$-\frac{1}{2}$ $-\frac{1}{3}$ $\frac{1}{4}$
11. 若有理数$a$,$b$在数轴上的对应点如图1.2.5-1所示,比较大小:
$\vert a\vert$
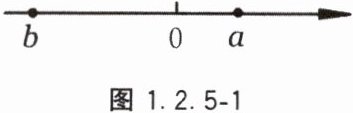
$\vert a\vert$
<
$-b$,$a$<
$\vert -b\vert$.
答案:
< <
12. 用“$<$”把下列各数按从小到大的顺序连接起来:
(1) $-5\frac{1}{2}$,$-\vert -4\vert$,$2$,$0$,$-2\frac{1}{3}$;
(2) $2.3$,$-0.15$,$0$,$-\frac{1}{3}$,$-1.5$,$-0.6$.
(1) $-5\frac{1}{2}$,$-\vert -4\vert$,$2$,$0$,$-2\frac{1}{3}$;
(2) $2.3$,$-0.15$,$0$,$-\frac{1}{3}$,$-1.5$,$-0.6$.
答案:
(1)$-5\frac{1}{2}<-|-4|<-2\frac{1}{3}<0<2$(2)$-1.5<-0.6<-\frac{1}{3}<-0.15<0<2.3$
13. (1) 求$\vert\frac{1}{10}-\frac{1}{11}\vert+\vert\frac{1}{11}-\frac{1}{12}\vert+\cdots+\vert\frac{1}{49}-\frac{1}{50}\vert$的值;
(2) 求$\vert\frac{1}{11}-\frac{1}{10}\vert+\vert\frac{1}{12}-\frac{1}{11}\vert+\cdots+\vert\frac{1}{50}-\frac{1}{49}\vert$的值.
(2) 求$\vert\frac{1}{11}-\frac{1}{10}\vert+\vert\frac{1}{12}-\frac{1}{11}\vert+\cdots+\vert\frac{1}{50}-\frac{1}{49}\vert$的值.
答案:
(1)$\frac{2}{25}$ (2)$\frac{2}{25}$
14. 已知$a$,$b$两数在数轴上的位置如图1.2.5-2所示,试在数轴上画出$-a$,$-b$两数的所在位置,并用“$<$”把这四个数连接起来.
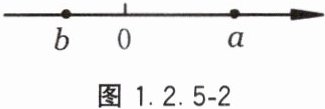

答案:
图略,$-a<b<-b<a$
15. 已知实数$a$在数轴上对应点的位置如图1.2.5-3所示. 若实数$b$满足$-a < b < a$,则$b$的值不可能是下列四个数中的(
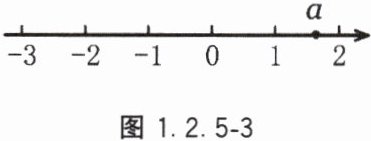
A.$1$
B.$0$
C.$-1$
D.$-2$
D
).
A.$1$
B.$0$
C.$-1$
D.$-2$
答案:
D
16. 我们把不超过有理数$x$的最大整数称为$x$的整数部分,记作$\lfloor x\rfloor$,又把$x - \lfloor x\rfloor$称为$x$的小数部分,记作$\{x\}$,则有$x=\lfloor x\rfloor+\{x\}$. 如:$\lfloor1.3\rfloor=1$,$\{1.3\}=0.3$,则有$1.3=\lfloor1.3\rfloor+\{1.3\}$. 现给出下列说法:① $\lfloor2.8\rfloor=2$;② $\lfloor -5.3\rfloor=-5$;③ $\{ -1.3\}=0.3$;④若$1<\vert x\vert<2$,且$\{x\}=0.4$,则$x=1.4$或$x=-1.4$. 其中说法正确的有(
A.$1$个
B.$2$个
C.$3$个
D.$4$个
A
).A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
A
查看更多完整答案,请扫码查看


