第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
四进制加法
6. 学习新知:
二进制加法法则:
$ 0 + 0 = 0 $ $ 0 + 1 = 1 $
$ 1 + 0 = 1 $ $ 1 + 1 = 10 $
拓展计算:
(1) 请依据以上运算法则,完成以下二进制数的加法运算:
$ (10)_2 + (1)_2 = $
$ (11)_2 + (1)_2 = $
(2) 请运用二进制运算法则进行十进制数的加法运算:
计算 $ 45 + 23 $;
第一步,把 45,23 分别转换为二进制数:
第二步,利用二进制数的加法运算法则计算它们的和:
第三步,将和转换为十进制数:
6. 学习新知:
二进制加法法则:
$ 0 + 0 = 0 $ $ 0 + 1 = 1 $
$ 1 + 0 = 1 $ $ 1 + 1 = 10 $
拓展计算:
(1) 请依据以上运算法则,完成以下二进制数的加法运算:
$ (10)_2 + (1)_2 = $
(11)₂
;$ (11)_2 + (1)_2 = $
(100)₂
.(2) 请运用二进制运算法则进行十进制数的加法运算:
计算 $ 45 + 23 $;
第一步,把 45,23 分别转换为二进制数:
(101101)₂,(10111)₂
;第二步,利用二进制数的加法运算法则计算它们的和:
(1000100)₂
;第三步,将和转换为十进制数:
68
.
答案:
6.(1)(11)₂(100)₂ (2)(101101)₂,(10111)₂ (1000100)₂ 68
五信息编码
信息编码,就是用少量、简单的基本符号,选用一定的组合规则,以表示大量复杂多样的信息.
7. 摩尔斯电码(Morse Code)也被称作摩斯密码,是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号. 它发明于 1837 年,是一种早期的数字化通信形式. 它的代码包括五种:短促的点信号“•”,保持一定时间的长信号“—”,表示点和划之间的停顿、每个词之间中等的停顿,以及句子之间长的停顿. 以下给出 26 个英文字母与摩斯码的对应表:
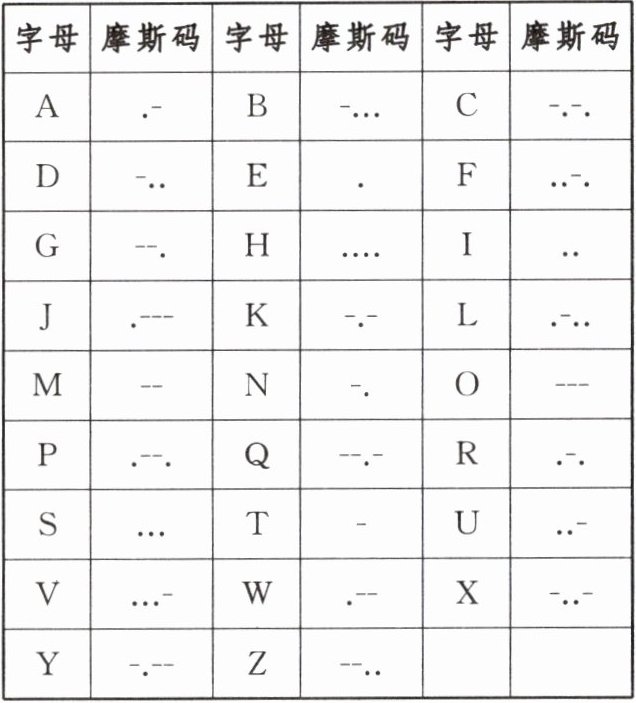
请同学们接收讯号,“.-.. ---...-.”的意思是
8. 信息编码在日常生活中处处都在使用,请查阅资料,说一说你的身份证号是如何编码的吧.
信息编码,就是用少量、简单的基本符号,选用一定的组合规则,以表示大量复杂多样的信息.
7. 摩尔斯电码(Morse Code)也被称作摩斯密码,是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号. 它发明于 1837 年,是一种早期的数字化通信形式. 它的代码包括五种:短促的点信号“•”,保持一定时间的长信号“—”,表示点和划之间的停顿、每个词之间中等的停顿,以及句子之间长的停顿. 以下给出 26 个英文字母与摩斯码的对应表:

请同学们接收讯号,“.-.. ---...-.”的意思是
LOVE
.8. 信息编码在日常生活中处处都在使用,请查阅资料,说一说你的身份证号是如何编码的吧.
答案:
7.LOVE
查看更多完整答案,请扫码查看


