第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 若$9x^{2}+ax+4$是一个完全平方式,则$a$的值为(
A.12
B.-12
C.12或-12
D.6或-6
C
)A.12
B.-12
C.12或-12
D.6或-6
答案:
C
2. 用配方法解下列方程,其中应在方程左右两边同时加上4的是(
A.$x^{2}-2x= 5$
B.$x^{2}+4x= 5$
C.$2x^{2}-4x= 5$
D.$4x^{2}+4x= 5$
B
)A.$x^{2}-2x= 5$
B.$x^{2}+4x= 5$
C.$2x^{2}-4x= 5$
D.$4x^{2}+4x= 5$
答案:
B
3. 下列用配方法解方程$\frac{1}{2}x^{2}-x-2= 0$的四个步骤中,出现错误的是(
$\frac{1}{2}x^{2}-x-2= 0→x^{2}-2x= 4→x^{2}-2x+1= 5→(x-1)^{2}= 5→x= \sqrt{5}+1$
① ② ③ ④
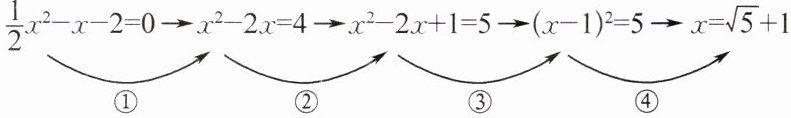
A.①
B.②
C.③
D.④
D
)$\frac{1}{2}x^{2}-x-2= 0→x^{2}-2x= 4→x^{2}-2x+1= 5→(x-1)^{2}= 5→x= \sqrt{5}+1$
① ② ③ ④
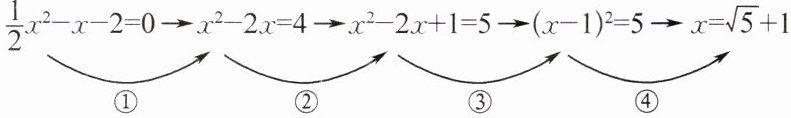
A.①
B.②
C.③
D.④
答案:
D
4. 将关于$x的一元二次方程x^{2}-px+q= 0$变形为$x^{2}= px-q$,就可以将$x^{2}表示为关于x$的一次多项式,从而达到“降次”的目的.例如:$x^{3}= x·x^{2}= x(px-q)=… $.我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知$x^{2}-x-1= 0$,且$x>0$,则代数式$x^{4}-2x^{3}+3x$的值为(
A.$1-\sqrt{5}$
B.$3-\sqrt{5}$
C.$1+\sqrt{5}$
D.$3+\sqrt{5}$
C
)A.$1-\sqrt{5}$
B.$3-\sqrt{5}$
C.$1+\sqrt{5}$
D.$3+\sqrt{5}$
答案:
C
5. 将一个一元二次方程$ax^{2}+bx+c= 0化为(x-m)^{2}= \frac{b^{2}-4ac}{4a^{2}}$,则$m$的值为
$-\frac{b}{2a}$
.
答案:
$-\frac{b}{2a}$
6. 代数式$2x^{2}-7x+2$的最小值为
$-\frac{33}{8}$
.
答案:
$-\frac{33}{8}$
7. 用配方法解方程$2y^{2}-\sqrt{5}y= 1$时,二次项系数化为1后方程两边都应加上
$\frac{5}{16}$
.
答案:
$\frac{5}{16}$
8. 贝贝用配方法解方程$2x^{2}-bx+a= 0$,若解得$x-\frac{3}{2}= \pm \frac{\sqrt{15}}{2}$,则$a$的值为
-3
.
答案:
-3 提示:因为$x-\frac{3}{2}=\pm\frac{\sqrt{15}}{2}$,所以$(x-\frac{3}{2})^{2}=\frac{15}{4}$,所以$x^{2}-3x+\frac{9}{4}=\frac{15}{4}$.整理,得$2x^{2}-6x-3=0$,所以$a=-3$.
9. 用配方法解下列方程:
(1)$-x^{2}+x+1= 0$;
(2)$-\frac{1}{3}x^{2}+2x+1= 0$.
(1)$-x^{2}+x+1= 0$;
(2)$-\frac{1}{3}x^{2}+2x+1= 0$.
答案:
(1)方程两边同时除以-1,得$x^{2}-x-1=0$.移项,得$x^{2}-x=1$.配方,得$x^{2}-x+(\frac{1}{2})^{2}=1+(\frac{1}{2})^{2}$,即$(x-\frac{1}{2})^{2}=\frac{5}{4}$.直接开平方,得$x-\frac{1}{2}=\pm\frac{\sqrt{5}}{2}$.所以$x_{1}=\frac{\sqrt{5}}{2}+\frac{1}{2}$,$x_{2}=-\frac{\sqrt{5}}{2}+\frac{1}{2}$;
(2)方程两边同时乘-3,得$x^{2}-6x-3=0$.移项,得$x^{2}-6x=3$.配方,得$x^{2}-6x+9=3+9$,即$(x-3)^{2}=12$.直接开平方,得$x-3=\pm2\sqrt{3}$.所以$x_{1}=3+2\sqrt{3},x_{2}=3-2\sqrt{3}$
(1)方程两边同时除以-1,得$x^{2}-x-1=0$.移项,得$x^{2}-x=1$.配方,得$x^{2}-x+(\frac{1}{2})^{2}=1+(\frac{1}{2})^{2}$,即$(x-\frac{1}{2})^{2}=\frac{5}{4}$.直接开平方,得$x-\frac{1}{2}=\pm\frac{\sqrt{5}}{2}$.所以$x_{1}=\frac{\sqrt{5}}{2}+\frac{1}{2}$,$x_{2}=-\frac{\sqrt{5}}{2}+\frac{1}{2}$;
(2)方程两边同时乘-3,得$x^{2}-6x-3=0$.移项,得$x^{2}-6x=3$.配方,得$x^{2}-6x+9=3+9$,即$(x-3)^{2}=12$.直接开平方,得$x-3=\pm2\sqrt{3}$.所以$x_{1}=3+2\sqrt{3},x_{2}=3-2\sqrt{3}$
10. 阅读材料:数学课上,吴老师在求代数式$x^{2}-4x+5$的最小值时,利用公式$a^{2}\pm 2ab+b^{2}= (a\pm b)^{2}$,对式子作如下变形:$x^{2}-4x+5= x^{2}-4x+4+1= (x-2)^{2}+1$,因为$(x-2)^{2}\geq 0$,所以$(x-2)^{2}+1\geq 1$.当$x= 2$时,$(x-2)^{2}+1= 1$,因此$(x-2)^{2}+1$有最小值1,即$x^{2}-4x+5$的最小值为1.
通过阅读材料,解答下列问题:
(1)代数式$x^{2}+6x+12$的最小值为______
(2)求代数式$-x^{2}+2x+9$的最大或最小值.
(3)试比较代数式$3x^{2}-2x与2x^{2}+3x-7$的大小,并说明理由.
通过阅读材料,解答下列问题:
(1)代数式$x^{2}+6x+12$的最小值为______
3
.(2)求代数式$-x^{2}+2x+9$的最大或最小值.
$-x^{2}+2x+9=-(x-1)^{2}+10$.因为$(x-1)^{2}\geq0$,所以$-(x-1)^{2}+10\leq10$.当$x=1$时,$-(x-1)^{2}+10$有最大值10,即代数式$-x^{2}+2x+9$的最大值为10
(3)试比较代数式$3x^{2}-2x与2x^{2}+3x-7$的大小,并说明理由.
因为$(3x^{2}-2x)-(2x^{2}+3x-7)=x^{2}-5x+7=(x-\frac{5}{2})^{2}+\frac{3}{4}\geq\frac{3}{4}>0$,所以$3x^{2}-2x>2x^{2}+3x-7$
答案:
(1)3 提示:$x^{2}+6x+12=(x+3)^{2}+3$.因为$(x+3)^{2}\geq0$,所以$(x+3)^{2}+3\geq3$.当$x=-3$时,$(x+3)^{2}+3$有最小值3,即代数式$x^{2}+6x+12$的最小值为3;
(2)$-x^{2}+2x+9=-(x-1)^{2}+10$.因为$(x-1)^{2}\geq0$,所以$-(x-1)^{2}+10\leq10$.当$x=1$时,$-(x-1)^{2}+10$有最大值10,即代数式$-x^{2}+2x+9$的最大值为10;
(3)因为$(3x^{2}-2x)-(2x^{2}+3x-7)=x^{2}-5x+7=(x-\frac{5}{2})^{2}+\frac{3}{4}\geq\frac{3}{4}>0$,所以$3x^{2}-2x>2x^{2}+3x-7$
(1)3 提示:$x^{2}+6x+12=(x+3)^{2}+3$.因为$(x+3)^{2}\geq0$,所以$(x+3)^{2}+3\geq3$.当$x=-3$时,$(x+3)^{2}+3$有最小值3,即代数式$x^{2}+6x+12$的最小值为3;
(2)$-x^{2}+2x+9=-(x-1)^{2}+10$.因为$(x-1)^{2}\geq0$,所以$-(x-1)^{2}+10\leq10$.当$x=1$时,$-(x-1)^{2}+10$有最大值10,即代数式$-x^{2}+2x+9$的最大值为10;
(3)因为$(3x^{2}-2x)-(2x^{2}+3x-7)=x^{2}-5x+7=(x-\frac{5}{2})^{2}+\frac{3}{4}\geq\frac{3}{4}>0$,所以$3x^{2}-2x>2x^{2}+3x-7$
查看更多完整答案,请扫码查看


