第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 已知关于x的一元二次方程$ax^2+bx+c= 0(a≠0).$若9a+3b+c= 0,则该方程一定有一个根为 (
A.-3
B.3
C.±3
D.不能确定
B
)A.-3
B.3
C.±3
D.不能确定
答案:
B
2. 已知$(m-3)x^m^2-7+2024x-2024= 0$是关于x的一元二次方程,则m的值为 (
A.3
B.0
C.-3
D.±3
C
)A.3
B.0
C.-3
D.±3
答案:
C
3. 若关于x的一元二次方程$ax^2+bx= c(ac≠0)$有一个实数根为2024,则关于x的方程$cx^2+bx= a$一定有一个实数根为 (
A.2024
B.1/2024
C.-2024
D.-1/2024
D
)A.2024
B.1/2024
C.-2024
D.-1/2024
答案:
D 提示:由条件,得a×2024²+2024b=c.两边同时除以2024²,得a+$\frac{1}{2024}$b=$(\frac{1}{2024})^2$c,即$(\frac{1}{2024})^2$c-$\frac{1}{2024}$b=a,即c$(-\frac{1}{2024})^2$+b$(-\frac{1}{2024})$=a.所以关于x的方程cx²+bx=a一定有一个实数根为-$\frac{1}{2024}$.
4. 如图,某小区在一块长16m、宽9m的矩形空地上新修三条宽度相同的小路,其中一条和矩形的一边平行,另外两条和矩形的另一边平行,空地剩下的部分种植花草,使得花草区域占地面积为$120m^2.$设小路的宽度为x m,现给出下列方程:①(16-2x)(9-x)= 120;②16×9-9×2x-(16-2x)x= 120;$③16×9-9×2x-16x+x^2= 120.$其中正确的是 (
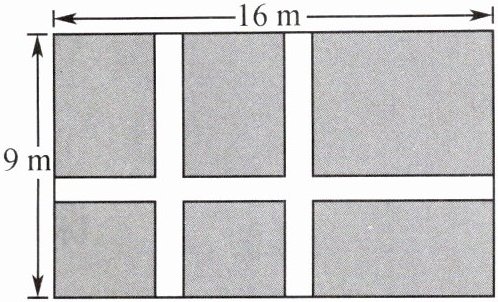
A.①
B.②
C.①②
D.①②③
C
)
A.①
B.②
C.①②
D.①②③
答案:
C
5. 若m是方程$x^2+x-1= 0$的一个根,则代数式$m^3+2m^2-7$的值是
-6
.
答案:
-6 提示:由题意,得m²+m=1,所以m³+2m²-7=m³+m²+m²-7=m(m²+m)+m²-7=-6.
6. 关于x的一元二次方程$a_1(x-m)^2+k= 0$与$a_2(x-m)^2+k= 0$称为“同族二次方程”.例如:$2(x-3)^2+4= 0$与$3(x-3)^2+4= 0$是“同族二次方程”.现有关于x的一元二次方程$2(x-1)^2+1= 0$与$(a+2)x^2+(b-4)·x+8= 0$是“同族二次方程”,那么代数式ab的值为______
-50
.
答案:
-50 提示:由题意,易得(a+2)x²+(b-4)x+8=(a+2)(x-1)²+1,即(a+2)x²+(b-4)x+8=(a+2)x²-2(a+2)x+a+3,所以$\begin{cases}-2(a+2)=b-4,\\a+3=8,\end{cases}$解得$\begin{cases}a=5,\\b=-10.\end{cases}$所以ab=-50.
7. 在一元二次方程$x^2-2ax+b= 0$中,若$a^2-b>0,$则称a是该方程的中点值.
(1)方程$x^2-10x+1= 0$的中点值是多少?
(2)已知方程$x^2-mx+n= 0$的中点值是3,且其中一个根是1,求mn的值.
(1)方程$x^2-10x+1= 0$的中点值是多少?
(2)已知方程$x^2-mx+n= 0$的中点值是3,且其中一个根是1,求mn的值.
答案:
解:
(1)由题意,得2a=10,解得a=5.又因为5²-1=24>0,所以方程x²-10x+1=0的中点值是5.
(2)由题意,得$\frac{1}{2}$m=3,解得m=6,所以方程为x²-6x+n=0.把x=1代入,得n=5.经检验,3²-5=4>0,所以m=6,n=5符合题意,所以mn=30.
(1)由题意,得2a=10,解得a=5.又因为5²-1=24>0,所以方程x²-10x+1=0的中点值是5.
(2)由题意,得$\frac{1}{2}$m=3,解得m=6,所以方程为x²-6x+n=0.把x=1代入,得n=5.经检验,3²-5=4>0,所以m=6,n=5符合题意,所以mn=30.
查看更多完整答案,请扫码查看


