第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. (2024德州市中考)甲、乙、丙三名射击运动员分别进行了5次射击训练,成绩(单位:环)如下表所示:
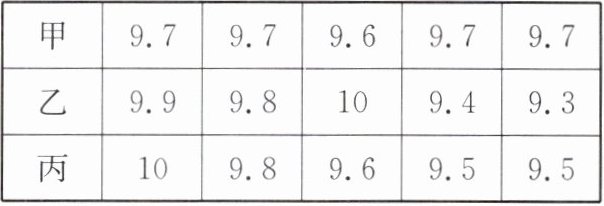
则三名运动员中成绩最稳定的是(
A.甲
B.乙
C.丙
D.无法确定

则三名运动员中成绩最稳定的是(
A
)A.甲
B.乙
C.丙
D.无法确定
答案:
A
2. 第1组数据为0,0,0,1,1;第2组数据为$\underbrace{0,0,…,0}_{m个0}$,$\underbrace{1,1,…,1}_{n个1}$,其中m,n是正整数. 现有下列结论:①当m= n时,两组数据的平均数相等;②当m>n时,第1组数据的平均数小于第2组数据的平均数;③当m<n时,第1组数据的中位数小于第2组数据的中位数;④当m= n时,第2组数据的方差小于第1组数据的方差. 其中正确的是(
A.①②
B.①③
C.①④
D.③④
B
)A.①②
B.①③
C.①④
D.③④
答案:
B 提示:第1组数据的平均数为$\frac{3}{6}=\frac{1}{2}$;第2组数据的平均数为$\frac{n}{m+n}$.当m=n时,$\frac{n}{m+n}=\frac{1}{2}$;当m>n时,$m+n>2n$,$\frac{n}{m+n}<\frac{1}{2}$.故①正确、②错误.第1组数据的中位数为$\frac{0+1}{2}=\frac{1}{2}$.当m<n时,若m+n为奇数,中位数为1;若m+n为偶数,中位数为1.故第2组数据的中位数为1,故③正确.第1组数据的方差为$s_{1}^{2}=\frac{1}{4}$.当m=n时,第2组数据的方差为$s_{2}^{2}=\frac{1}{m+n}[m(0-\frac{1}{2})^{2}+n(1-\frac{1}{2})^{2}]=\frac{1}{4}$,故④错误.
3. 一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字. 根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是(
A.中位数是3,众数是2
B.平均数是3,中位数是2
C.平均数是3,方差是2
D.平均数是3,众数是2
C
)A.中位数是3,众数是2
B.平均数是3,中位数是2
C.平均数是3,方差是2
D.平均数是3,众数是2
答案:
C 提示:本题采用举反例和排除法解之.选项A,如2,2,3,4,6;选项B与D,如2,2,2,3,6,故选C.对于选项C,由方差$\frac{1}{5}[(x_{1}-3)^{2}+(x_{2}-3)^{2}+\cdots+(x_{5}-3)^{2}]=2$可知,这5个数字中至多出现一次6,不妨记$x_{5}=6$,则$(x_{1}-3)^{2}+(x_{2}-3)^{2}+\cdots+(x_{4}-3)^{2}=1$.所以其余4个数字只能为2,3,3,3或3,3,3,4.又因$x_{1}+x_{2}+x_{3}+x_{4}+6=3×5=15$,即$x_{1}+x_{2}+x_{3}+x_{4}=9$,而2+3+3+3=11≠9,3+3+3+4=13≠9,故这5个数字中一定没有出现数字6.
4. 若一组数据2,3,4,5,x的方差比另一组数据5,6,7,8,9的方差小,则x的值可以为
2
(写出一个满足条件的值).
答案:
2(答案不唯一) 提示:数据5,6,7,8,9中,每相邻2个数相差1,数据2,3,4,5,x中,前4个数据每相邻2个数也相差1,所以当x=1或x=6时,两组数据的方差相等.因为数据2,3,4,5,x的方差比另一组数据5,6,7,8,9的方差小,所以1<x<6,所以x在1至6范围内(不包含1,6)任取一数即可.
5. (2024山西省中考)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛. 各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.
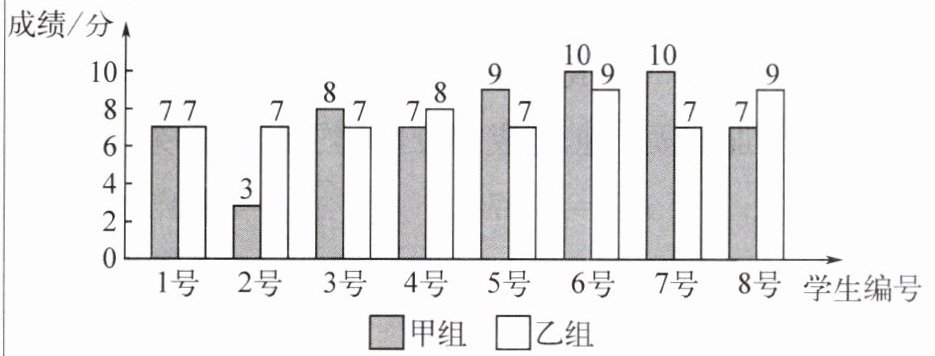
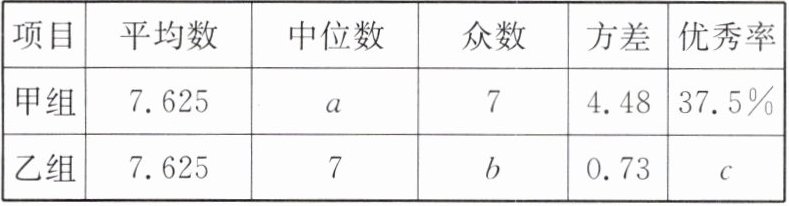
数据分析:小夏对这两个小组的成绩进行了如下分析:
请认真阅读上述信息,回答下列问题:
(1)填空:a=
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好. 小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.

数据分析:小夏对这两个小组的成绩进行了如下分析:

请认真阅读上述信息,回答下列问题:
(1)填空:a=
7.5
,b= 7
,c= 25%
.(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好. 小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②甲组成绩的中位数为7.5,高于乙组成绩的中位数,所以从中位数的角度看,甲组成绩比乙组好.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
答案:
(1) 7.5 7 25%
(2) 理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②甲组成绩的中位数为7.5,高于乙组成绩的中位数,所以从中位数的角度看,甲组成绩比乙组好.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
(1) 7.5 7 25%
(2) 理由不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②甲组成绩的中位数为7.5,高于乙组成绩的中位数,所以从中位数的角度看,甲组成绩比乙组好.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
查看更多完整答案,请扫码查看


