第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 在 Rt△ABC 中,∠C= 90°,AC= 3,BC= 4,以 AC 所在直线为轴,把△ABC 旋转一周,得到圆锥,则该圆锥的侧面积为(
A.12π
B.15π
C.20π
D.24π
C
)A.12π
B.15π
C.20π
D.24π
答案:
C
2. 用一个直径为 10 cm 的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁轴截面如图所示,圆锥的母线 AB 与⊙O 相切,不倒翁的顶点 A 到桌面 L 的最大距离是 18 cm. 若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为(
$A.60π cm^2$
B.$\frac{600π}{13}$ cm^2
C.$\frac{720π}{13}$ cm^2
$D.72π cm^2$
]
C
)$A.60π cm^2$
B.$\frac{600π}{13}$ cm^2
C.$\frac{720π}{13}$ cm^2
$D.72π cm^2$
]
答案:
C 提示:设题图中的另一个切点为E,连接BE交OA于点D,连接OB. 由题意,得OB=5cm,AO=18 - 5=13(cm). 由勾股定理,得AB=$\sqrt{AO^{2}-OB^{2}}$=12cm. 因为$\frac{1}{2}$BD·AO=$\frac{1}{2}$AB·OB,所以BD=$\frac{60}{13}$cm. 所以涂色部分的面积为π×$\frac{60}{13}$×12=$\frac{720π}{13}$($cm^{2}$).
3. 如图,C 为扇形 OAB 的半径 OB 上一点,将△OAC 沿 AC 折叠,点 O 恰好落在$\widehat{AB}$上的点 D 处,且$l_{\widehat{BD}}:l_{\widehat{AD}}= 1:3$($l_{\widehat{BD}}表示\widehat{BD}$的长). 若将扇形 OAB 围成一个圆锥,则该圆锥的底面圆半径与母线长的比为( )
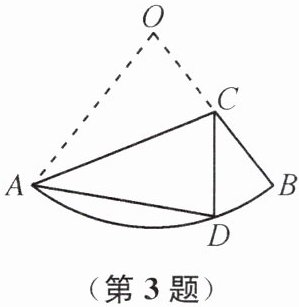
A.1:3
B.1:π
C.1:4
D.2:9
D

A.1:3
B.1:π
C.1:4
D.2:9
答案:
D 提示:连接OD交AC于点M. 由折叠,得OM=$\frac{1}{2}$OD=$\frac{1}{2}$OA,∠OMA=90°,所以∠OAM=30°,所以∠AOM=60°. 因为$l_{\widehat{BD}}$:$l_{\widehat{AD}}$=1:3,所以∠BOD=20°,所以∠AOB=∠AOM+∠BOD=80°. 设该圆锥的底面圆半径为r,母线长为l. 因为$\frac{80πl}{180}$=2πr,所以r:l=2:9.
4. 如图是一纸杯,它的母线 AC 和 EF 延长后形成的立体图形是圆锥. 该圆锥的侧面展开图形是扇形 OAB. 经测量,纸杯上开口圆的直径为 6 cm,下底面直径为 4 cm,母线长 EF= 8 cm. 则这个纸杯的表面积是$
44π
cm^2($结果保留π).
答案:
44π 提示:由题意可知,$\widehat{BA}$=6πcm,$\widehat{CD}$=4πcm. 设∠AOB=$n^{\circ}$,AO=Rcm,则CO=(R - 8)cm. 由弧长公式,得$\frac{nπR}{180}$=6π,$\frac{nπ(R - 8)}{180}$=4π,所以$\begin{cases}6×180=nR\\4×180=nR - 8n\end{cases}$,解得n=45,R=24,故扇形OAB的圆心角是45°. 因为R=24,R - 8=16,所以$S_{扇形OCD}$=$\frac{1}{2}$×4π×16=32π($cm^{2}$),$S_{扇形OAB}$=$\frac{1}{2}$×6π×24=72π($cm^{2}$),所以纸杯侧面积=$S_{扇形OAB}$ - $S_{扇形OCD}$=72π - 32π=40π($cm^{2}$),纸杯底面积=π×$2^{2}$=4π($cm^{2}$),所以纸杯表面积=40π + 4π=44π($cm^{2}$).
5. 王师傅要制作一个圆锥模型,操作规则是:在一块边长为 16 cm 的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面. 王师傅首先设计了如图所示的方案一,但发现这个方案不可行,于是他调整了扇形和圆的半径,设计了如图所示的方案二(两个方案的图中,圆与正方形相邻的两边及扇形的弧均相切. 方案一中扇形的弧与正方形的两边相切).
(1)请说明方案一不可行的理由.
(2)判断方案二是否可行. 若可行,请求出圆锥的母线长 l 及其底面圆的半径 r;若不可行,请说明理由.
]

(1)请说明方案一不可行的理由.
(2)判断方案二是否可行. 若可行,请求出圆锥的母线长 l 及其底面圆的半径 r;若不可行,请说明理由.
]

答案:
解:
(1) 连接AC,则易证A,M,$O_1$,C四点共线. 设⊙$O_1$的半径为r cm,则$\frac{90}{180}$×π×16=2πr,解得r=4. 过点$O_1$作$O_1$H⊥CD于点H,则$O_1$H=4 cm,所以$O_1$C=$\sqrt{4^{2}+4^{2}}$=4$\sqrt{2}$(cm). 因为AM=AB=16 cm,所以制作这样的圆锥实际需要正方形纸片对角线的长为16 + 4 + 4$\sqrt{2}$=(20 + 4$\sqrt{2}$)cm. 因为20 + 4$\sqrt{2}$>16$\sqrt{2}$,所以方案一不可行.
(2) 方案二可行.
根据题意,得(1 + $\sqrt{2}$)r + l=16$\sqrt{2}$①,2πr=$\frac{90}{180}$πl②. 由①②可得,l=$\frac{320\sqrt{2}-128}{23}$,r=$\frac{80\sqrt{2}-32}{23}$.
答:所求圆锥的母线长l为$\frac{320\sqrt{2}-128}{23}$cm,底面圆的半径r为$\frac{80\sqrt{2}-32}{23}$cm.
(1) 连接AC,则易证A,M,$O_1$,C四点共线. 设⊙$O_1$的半径为r cm,则$\frac{90}{180}$×π×16=2πr,解得r=4. 过点$O_1$作$O_1$H⊥CD于点H,则$O_1$H=4 cm,所以$O_1$C=$\sqrt{4^{2}+4^{2}}$=4$\sqrt{2}$(cm). 因为AM=AB=16 cm,所以制作这样的圆锥实际需要正方形纸片对角线的长为16 + 4 + 4$\sqrt{2}$=(20 + 4$\sqrt{2}$)cm. 因为20 + 4$\sqrt{2}$>16$\sqrt{2}$,所以方案一不可行.
(2) 方案二可行.
根据题意,得(1 + $\sqrt{2}$)r + l=16$\sqrt{2}$①,2πr=$\frac{90}{180}$πl②. 由①②可得,l=$\frac{320\sqrt{2}-128}{23}$,r=$\frac{80\sqrt{2}-32}{23}$.
答:所求圆锥的母线长l为$\frac{320\sqrt{2}-128}{23}$cm,底面圆的半径r为$\frac{80\sqrt{2}-32}{23}$cm.
查看更多完整答案,请扫码查看


